
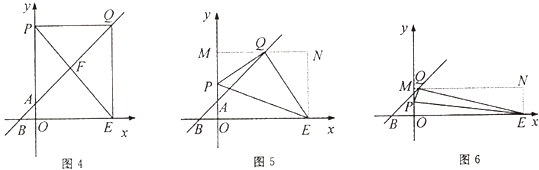
����Ŀ����ͼ��������y=ax2+c��a��0����y�ύ�ڵ�A����x�ύ��B��C���㣨��C��x���������ϣ�����ABCΪ����ֱ�������Σ������Ϊ4���ֽ���������BA����ƽ�ƣ�ƽ�ƺ�������߹���Cʱ����x�����һ��ΪE���䶥��ΪF���Գ�����x��Ľ���ΪH��
��1����a��c��ֵ��
��2������OF�����жϡ�OEF�Ƿ�Ϊ���������Σ���˵�����ɣ�
��3���ֽ�һ�㹻������ǰ��ֱ�Ƕ���Q��������AF������HF�ϣ�һֱ�DZ�ʼ�չ���E����һֱ�DZ���y���ཻ�ڵ�P���Ƿ���������ĵ�Q��ʹ�Ե�P��Q��EΪ��������������POEȫ�ȣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��������y=ax2+c��a��0����y�ύ�ڵ�A��
��A��0��c������OA=c��
�ߡ�ABCΪ����ֱ�������Σ�
��OA=OB=OC=c��
�� ![]() c2c=4�����c=2��
c2c=4�����c=2��
��C��2��0����
��C��2��0������y=ax2+2��4a+2=0�����a=�� ![]()
��2��
�⣺��OEF�ǵ��������Σ��������£���ͼ1��

��ֱ��AB�Ľ���ʽΪy=kx+b��
��A��0��2����B����2��0������� ![]() �����
����� ![]() ��
��
��ֱ��AB�Ľ���ʽΪy=x+2��
��F��t��t+2����
��������y=�� ![]() x2+2��BA����ƽ�ƣ�ƽ�ƺ�������߹���Cʱ������ΪF��
x2+2��BA����ƽ�ƣ�ƽ�ƺ�������߹���Cʱ������ΪF��
��ƽ�ƺ�������߽���ʽΪy=�� ![]() ��x��t��2+t+2��
��x��t��2+t+2��
��C��2��0������é� ![]() ��2��t��2+t+2=0�����t=6��
��2��t��2+t+2=0�����t=6��
��ƽ�ƺ�������߽���ʽΪy=�� ![]() ��x��6��2+8��
��x��6��2+8��
��F��6��8����
��OF= ![]() =10��
=10��
��y=0���� ![]() ��x��6��2+8=0�����x1=2��x2=10��
��x��6��2+8=0�����x1=2��x2=10��
��OE=10��
��OE=OF��
���OEF����������
��3��
�⣺���ڣ���Q��λ�÷��������Σ�
����һ����Q������HF�ϣ�
����P��x���Ϸ�ʱ����ͼ2��
�ߡ�EQP=90�㣬EP=EP��
�൱EQ=EO=10ʱ����EQP�ա�EOP��
��HE=10��6=4��
��QH= ![]() =2
=2 ![]() ��
��
��ʱQ������Ϊ��6��2 ![]() ����
����
����P��x���·�ʱ����ͼ3����PQ=OE=10����P����PK��HF�ڵ�K������PK=6��
��Rt��PQK��QK= ![]() =
= ![]() =8��
=8��
�ߡ�PQE=90�㣬���PQK+HQE=90�㣬
�ߡ�PKQ=��QHE=90�㣬
���PKQ�ס�QHE��
�� ![]() ����
���� ![]() �����QH=3��
�����QH=3��
��Q��6��3����

���ζ�����Q������AF�ϣ�
��PQ=OE=10ʱ����ͼ4����QE=PO��
���ı���POEQΪ���Σ���Q�ĺ�����Ϊ10��
��x=10ʱ��y=x+2=12����Q��10��12����
��QE=OE=10ʱ����ͼ5��
��Q��QM��y���ڵ�M����E����x��Ĵ��߽�QM�ڵ�N��
��Q������ΪΪ��x��x+2������MQ=x��QN=10��x��EN=x+2��
��Rt��QEN����QE2=QN2+EN2����102=��10��x��2+��x+2��2�����x=4�� ![]() ��
��
��x=4+ ![]() ʱ����ͼ5��y=x+2=6+
ʱ����ͼ5��y=x+2=6+ ![]() ����Q��4+
����Q��4+ ![]() ��6+
��6+ ![]() ����
����
��x=4�� ![]() ʱ����ͼ5��y=x+2=6��
ʱ����ͼ5��y=x+2=6�� ![]() ����Q��4��
����Q��4�� ![]() ��6��
��6�� ![]() ����
����
����������Q���������6��2 ![]() ����6��3����10��12����4+
����6��3����10��12����4+ ![]() ��6+
��6+ ![]() ����4��
����4�� ![]() ��6��
��6�� ![]() ����ʹP��Q��E����Ϊ��������������POEȫ��
����ʹP��Q��E����Ϊ��������������POEȫ��
����������1�������A��0��c������OA=c���ٸ��ݵ���ֱ�������ε����ʵ�OA=OB=OC=c�����������������ʽ�� ![]() c2c=4�����c=2�����Ű�C��2��0������y=ax2+2�����a��ֵ����2����ͼ1�������ô���ϵ�������ֱ��AB�Ľ���ʽΪy=x+2����F��t��t+2��������������ƽ�ƵĹ��ɿ���ƽ�ƺ�������߽���ʽΪy=��
c2c=4�����c=2�����Ű�C��2��0������y=ax2+2�����a��ֵ����2����ͼ1�������ô���ϵ�������ֱ��AB�Ľ���ʽΪy=x+2����F��t��t+2��������������ƽ�ƵĹ��ɿ���ƽ�ƺ�������߽���ʽΪy=�� ![]() ��x��t��2+t+2���ٰ�C��2��0������é�
��x��t��2+t+2���ٰ�C��2��0������é� ![]() ��2��t��2+t+2=0���ɽ��t=6����ƽ�ƺ�������߽���ʽΪy=��
��2��t��2+t+2=0���ɽ��t=6����ƽ�ƺ�������߽���ʽΪy=�� ![]() ��x��6��2+8������F��6��8�������ù��ɶ��������OF=10�����Ÿ�����������x��Ľ�������ȷ��E��10��0������OE=OF=10�����ǿ��жϡ�OEFΪ���������Σ���3���������ۣ�����Q������HF�ϣ���ͼ2������������ȫ�ȵ��ж���������EQ=EO=10ʱ����EQP�ա�EOP����ɸ��ݹ��ɶ��������QH=2
��x��6��2+8������F��6��8�������ù��ɶ��������OF=10�����Ÿ�����������x��Ľ�������ȷ��E��10��0������OE=OF=10�����ǿ��жϡ�OEFΪ���������Σ���3���������ۣ�����Q������HF�ϣ���ͼ2������������ȫ�ȵ��ж���������EQ=EO=10ʱ����EQP�ա�EOP����ɸ��ݹ��ɶ��������QH=2 ![]() �����ǿɵ�Q������Ϊ��6��2
�����ǿɵ�Q������Ϊ��6��2 ![]() ��������Q������AF�ϣ���ͼ3������������ȫ�ȵ��ж���������EQ=EO=10ʱ����EQP�ա�EOP����Q��m��m+2�������������ľ��빫ʽ�õ���m��10��2+��m+2��2=102 �� �ⷽ�����m��ֵ���ɵõ�Q�����꣮
��������Q������AF�ϣ���ͼ3������������ȫ�ȵ��ж���������EQ=EO=10ʱ����EQP�ա�EOP����Q��m��m+2�������������ľ��빫ʽ�õ���m��10��2+��m+2��2=102 �� �ⷽ�����m��ֵ���ɵõ�Q�����꣮
�����㾫����������Ҫ�����˶��κ��������ʵ����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ACΪ��O��ֱ����BΪ��O��һ�㣬��ACB=30�㣬�ӳ�CB����D��ʹ��CB=BD������D��DE��AC������E��CA���ӳ����ϣ�����BE�� 
��1����֤��BE�ǡ�O�����ߣ�
��2����BE=3ʱ����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У�E��F�ǶԽ���BD�ϵ����㣬�������һ��������ʹ��ABE�ա�CDF�������ӵ���������Ϊ�� �� 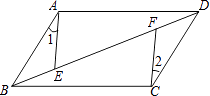
A.BE=DF
B.BF=DE
C.AE=CF
D.��1=��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�EΪCD���е㣬FΪBE�ϵ�һ�㣬����CF���ӳ���AB�ڵ�M��MN��CM������AD�ڵ�N�� 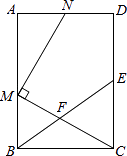
��1����FΪBE�е�ʱ����֤��AM=CE��
��2���� ![]() =2����
=2���� ![]() ��ֵ��
��ֵ��
��3���� ![]() =n����nΪ��ֵʱ��MN��BE��
=n����nΪ��ֵʱ��MN��BE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A�������ǣ�0��3������B��x���ϣ�����AOB�Ƶ�A��ʱ����ת90��õ���AEF����O��B�Ķ�Ӧ��ֱ��ǵ�E��F��
��1������B�������ǣ���4��0��������ͼ�л�����AEF����д����E��F�����꣮
��2������F����x����Ϸ�ʱ����д��һ�����������ĵ�B�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BC�ǡ�O��ֱ����AC�С�O�ڵ�C��AB����O�ڵ�D��EΪAC���е㣬����DE�� 
��1����AD=DB��OC=5��������AC�ij���
��2����֤��ED�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������κ���y1=a��x��x1����x��x2����a��0��x1��x2����ͼ����һ�κ���y2=dx+e��d��0����ͼ���ڵ㣨x1 �� 0����������y=y1+y2��ͼ����x�����һ�����㣬�� ��
A.a��x1��x2��=d
B.a��x2��x1��=d
C.a��x1��x2��2=d
D.a��x1+x2��2=d
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��F��������ABCD�ı�CD�ϵ�һ�����㣬BF�Ĵ�ֱƽ���߽��Խ���AC�ڵ�E������BE��FE�����EBF�Ķ����ǣ� �� 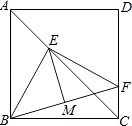
A.45��
B.50��
C.60��
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AC=8��BC=6��D��AB���е㣬��E�ڱ�AC�ϣ�����ADE��DE���ۣ�ʹ�õ�A���ڵ�A'������A'E��ACʱ��A'B= �� 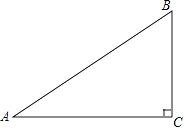
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com