
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的三个顶点的坐标分别是:A(2,2),B(1,0),C(3,1).
(1)画出△ABC关于x轴对称的△A′B′C′,并求出点A′、B′、C′的坐标.
(2)在坐标平面内是否存在点D,使得△COD为等腰三角形?若存在,直接写出点D的坐标(找出满足条件的两个点即可);若不存在,请说明理由.

【答案】(1)画图见解析,![]() (2,-2),
(2,-2),![]() (1,0),
(1,0),![]() (3,-1)
(3,-1)
(2)存在点D使得△COD为等腰三角形,
满足条件的点D在坐标轴上的坐标.D1(6,0);D2(![]() ,0);D3(
,0);D3(![]() ,0);D4(-
,0);D4(-![]() ,0);D5(0,5);D6(0,
,0);D5(0,5);D6(0,![]() );D7(0,2);D8(0,-
);D7(0,2);D8(0,-![]() );(答案不唯一,正确即可得分)
);(答案不唯一,正确即可得分)
【解析】
试题(1)按照条件画出即可,并根据关于X轴对称的点的特点写出点的坐标
(2)只要是线段OC垂直平分线上的点均满足条件,这样的点有很多
试题解析:(1)如图△![]() 即为所做的三角形.
即为所做的三角形.
其中![]() (2,-2),
(2,-2),![]() (1,0),
(1,0),![]() (3,-1).
(3,-1).
(2)存在点D使得△COD为等腰三角形,(答案不唯一,正确即可得分)
提示:如图所示,满足条件的点D在坐标轴上的坐标.D1(6,0);D2(![]() ,0);D3(
,0);D3(![]() ,0);D4(-
,0);D4(-![]() ,0);D5(0,5);D6(0,
,0);D5(0,5);D6(0,![]() );D7(0,2);D8(0,-
);D7(0,2);D8(0,-![]() );或垂直平分线
);或垂直平分线![]() 上任一点即可.
上任一点即可.




 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
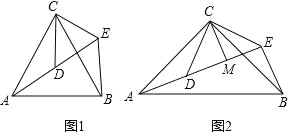
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠ACO= ![]() .
.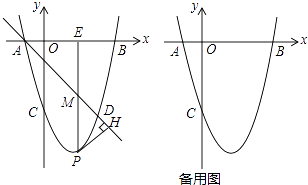
(1)求抛物线的解析式;
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值;
(3)在(2)的条件下,以点E为端点,在直线EP的右侧作一条射线与抛物线交于点N,使得∠NEP为锐角,在线段EB上是否存在点G,使得以E,N,G为顶点的三角形与△AOC相似?如果存在,请求出点G的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:EC,⑤OD2=DECD,正确的有( ) 
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,购进了甲、乙两种型号的新书柜来放置新买的图书,甲型号书柜共花了15000元,乙型号书柜共花了18000元,乙型号书柜比甲型号书柜单价便宜了300元,购买乙型号书柜的数量是甲型号书柜数量的2倍.求甲、乙型号书柜各购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,是一个长为 2m,宽为 2n 的长方形,沿图中虚线用剪刀将其均分成四个完全相同的小长方形,然后按图 2 的形状拼图.
(1)图 2 中的图形阴影部分的边长为 ;(用含 m、n 的代数式表示)
(2)请你用两种不同的方法分别求图 2 中阴影部分的面积; 方法一: ;方法二: .
(3)观察图 2,请写出代数式(m+n)2、(m﹣n)2、4mn 之间的关系式: .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com