
【题目】如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:EC,⑤OD2=DECD,正确的有( ) 
A.2个
B.3个
C.4个
D.5个
【答案】C
【解析】解:连接OE,如图所示:
∵AD与圆O相切,DC与圆O相切,BC与圆O相切,
∴∠DAO=∠DEO=∠OBC=90°,
∴DA=DE,CE=CB,AD∥BC,
∴CD=DE+EC=AD+BC,选项②正确;
在Rt△ADO和Rt△EDO中, ![]() ,
,
∴Rt△ADO≌Rt△EDO(HL),
∴∠AOD=∠EOD,
同理Rt△CEO≌Rt△CBO,
∴∠EOC=∠BOC,
又∠AOD+∠DOE+∠EOC+∠COB=180°,
∴2(∠DOE+∠EOC)=180°,即∠DOC=90°,选项①正确;
∴∠DOC=∠DEO=90°,又∠EDO=∠ODC,
∴△EDO∽△ODC,
∴ ![]() =
= ![]() ,即OD2=DCDE,选项⑤正确;
,即OD2=DCDE,选项⑤正确;
∵∠AOD+∠COB=∠AOD+∠ADO=90°,
∠A=∠B=90°,
∴△AOD∽△BOC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,选项③正确;
,选项③正确;
同理△ODE∽△OEC,
∴ ![]() ,选项④错误;
,选项④错误;
故选C.

连接OE,由AD,DC,BC都为圆的切线,根据切线的性质得到三个角为直角,且利用切线长定理得到DE=DA,CE=CB,由CD=DE+EC,等量代换可得出CD=AD+BC,选项②正确;由AD=ED,OD为公共边,利用HL可得出直角三角形ADO与直角三角形EDO全等,可得出∠AOD=∠EOD,同理得到∠EOC=∠BOC,而这四个角之和为平角,可得出∠DOC为直角,选项①正确;由∠DOC与∠DEO都为直角,再由一对公共角相等,利用两对对应角相等的两三角形相似,可得出三角形DEO与三角形DOC相似,由相似得比例可得出OD2=DECD,选项⑤正确;由△AOD∽△BOC,可得 ![]() =
= ![]() =
= ![]() =
= ![]() ,选项③正确;由△ODE∽△OEC,可得
,选项③正确;由△ODE∽△OEC,可得 ![]() ,选项④错误.
,选项④错误.


科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2014年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |

(1)表中的a=________,b=________;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,Rt△AOB的两条直角边OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.

(1)写出点A,B,C,D的坐标;
(2)求点A和点C之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的三个顶点的坐标分别是:A(2,2),B(1,0),C(3,1).
(1)画出△ABC关于x轴对称的△A′B′C′,并求出点A′、B′、C′的坐标.
(2)在坐标平面内是否存在点D,使得△COD为等腰三角形?若存在,直接写出点D的坐标(找出满足条件的两个点即可);若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明爸爸装修要粉刷断居室的墙面,在家装商场选购某品牌的乳胶漆:
规格(升/桶) | 价格(元/桶) | |
大桶装 | 18 | 225 |
小桶装 | 5 | 90 |
小明爸估算家里的粉刷面积,若买“大桶装”,则需若干桶但还差2升;若买“小桶装”,则需多买11桶但会剩余1升,
(1)小明爸预计墙面的粉刷需要乳胶漆多少升?
(2)喜迎新年,商场进行促销:满1000减120元现金,并且该品牌商家对“小桶装”乳胶漆有“买4送1“的促销活动,小明爸打算购买“小桶装”,比促销前节省多少钱?
(3)在(2)的条件下,商家在这次乳胶漆的销售买卖中,仍可盈利25%,则小桶装乳胶漆每桶的成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为 ![]() .其中,正确的结论是( )
.其中,正确的结论是( ) 
A.①②④
B.①③⑤
C.②③④
D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 我们定义:如图1、图2、图3,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB'C′是△ABC的“旋补三角形”,△AB′C′边B'C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.图1、图2、图3中的△AB′C′均是△ABC的“旋补三角形”.
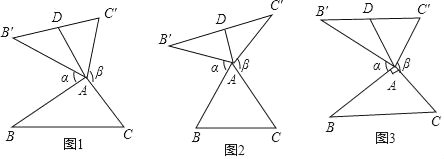
(1)①如图2,当△ABC为等边三角形时,“旋补中线”AD与BC的数量关系为:AD= BC;
②如图3,当∠BAC=90°,BC=8时,则“旋补中线”AD长为 .
(2)在图1中,当△ABC为任意三角形时,猜想“旋补中线”AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB'C′;
(2)画出△AB′C′向左平移4格后的△A′B″C″;
(3)计算线段AB在变换到AB′的过程中扫过区域的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com