
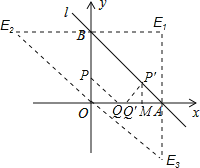
����Ŀ����ͼ��ֱ��l��������ֱ���A��B���㣬��BAO=45�㣬��A����Ϊ��8��0��������P�ӵ�O�����������߶�OBA�˶�������Aֹͣ��ͬʱ����QҲ�ӵ�O���������߶�OA�˶�������Aֹͣ�����ǵ��˶��ٶȾ�Ϊÿ��1����λ���ȣ�

��1����ֱ��AB�ĺ�����ϵʽ��
��2������A��B��O��ƽ���ڵ�E��ɵ�ͼ����ƽ���ı��Σ���ֱ��д����E�����ꣻ
��3�����˶������У���P��Q�ľ���Ϊ2ʱ�����P�����꣮
���𰸡���1��y=��x+8����2������������3��P�䣨8��![]() ��
��![]() ����
����
��������
�����������1����ֱ��AB����ʽΪy=kx+b����A��B����������k��b��ֵ������ȷ��������ʽ��
��2�����������������ͼ��ʾ���ı���AOBE1Ϊƽ���ı���ʱ���ı���ABE2OΪƽ���ı���ʱ���ı���ABOE3Ϊƽ���ı���ʱ���ֱ����E�����꼴�ɣ�
��3��������������ǣ���P��OB��ʱ������PQ������PQ�ij���������OPQΪ����ֱ�������Σ����OP�ij���ȷ������ʱP���ꣻ��P����AB��ʱ����P����P��M��x�ᣬȷ������ʱP�����꼴�ɣ�
�⣺��1���ߡ�BAO=45�㣬��AOB=90�㣬
���AOBΪ����ֱ�������Σ���OA=OB=8��
��B��0��8����
��ֱ��AB����ʽΪy=kx+b��
��A��8��0����B��0��8������ã�![]() ��
��
��ã�k=��1��b=8��
��ֱ��AB����ʽΪy=��x+8��
��2����ͼ��ʾ�����ı���AOBE1Ϊƽ���ı���ʱ��E1����Ϊ��8��8����
���ı���ABE2OΪƽ���ı���ʱ��E2����Ϊ����8��8����
���ı���ABOE3Ϊƽ���ı���ʱ��E3����Ϊ��8����8����
��3����P��OB��ʱ������PQ����PQ=2��
��Rt��POQ�У�OP=OQ���ɵã�OP=OQ=![]() ��2=
��2=![]() ����ʱP��0��
����ʱP��0��![]() ����
����
��P����AB��ʱ����P����P��M��x�ᣬ
��P��Q��=2����P��Q��MΪ����ֱ�������Σ�
��P��M=Q��M=![]() ��OM=OB��P��M=8��
��OM=OB��P��M=8��![]() ��
��
��ʱP�䣨8��![]() ��
��![]() ����
����


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC�У�OB��OC�ǡ�ABC����ACB�Ľ�ƽ���ߣ�
��1����д����ı���
��A�Ķ��� | 50�� | 60�� | 70�� |
��BOC�Ķ��� |
��2���Բ����A���BOC֮�����һ��������������ϵ����֤����IJ��룻
��3����ͼ2����ABC�ĸ�BE��CD����O�㣬��˵��ͼ�С�A���BOD�Ĺ�ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԪһ�η��̽�����⣺�ְ�����һ��ƻ���ؼң�С����ָ������ÿһ���ˣ����ÿ�˷�3������ʣ��3��ƻ���ֲ��꣬���ÿ�˷�4������2��ƻ���Ź��֣���С�����м����ˣ��ְ����˶��ٸ�ƻ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������45�ˣ�ij����ѧ���Գɼ�����λ���ֱ���88�ֺ�90�֣���90�ּ�90������Ϊ���㣬������������İ༶��________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
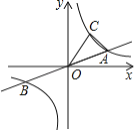
����Ŀ����ͼ����ֱ֪��y=![]() x��˫����y��
x��˫����y��![]() ��k��0������A��B���㣬��B������Ϊ����4����2����CΪ˫����y=
��k��0������A��B���㣬��B������Ϊ����4����2����CΪ˫����y=![]() ��k��0����һ�㣬���ڵ�һ�����ڣ�����AOC�����Ϊ6�����C������Ϊ ��
��k��0����һ�㣬���ڵ�һ�����ڣ�����AOC�����Ϊ6�����C������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AB��CD�����������������̽����APC���PAB����PCD��������ϵ��
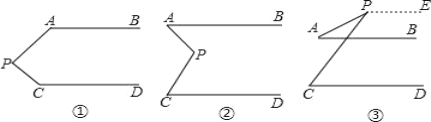
��1��ͼ���У���APC+��PAB+��PCD=�� �� ��
��2��ͼ���У����� ��
��3��ͼ���У�д����APC���PAB����PCD������������ϵ����˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������ABC�У�AB=AC��AD��BC������Ϊ��D��AN����ABC�����CAM��ƽ���ߣ�CE��AN������Ϊ��E������DE��AC�ڵ�F��

��1����֤���ı���ADCEΪ���Σ�
��2������ABC����ʲô����ʱ���ı���ADCE��һ�������Σ�������֤����
��3���ڣ�2���������£���AB=AC=2![]() ����������ADCE�ܳ���
����������ADCE�ܳ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com