һ�κ���y=kx+b��k��0����ͼ����һ��ֱ�ߣ�����x��Ľ��������ǣ�
-��0������y��Ľ��������ǣ�0��b����������ǰ�
-����һ�κ���ͼ����x���ϵĽؾ�m����b����һ�κ���ͼ����y���ϵĽؾ�n������
-����һ�κ���ͼ���б�ʣ�
���磺һ�κ���y=2x+2��ͼ����x��Ľ�������Ϊ��-1��0������y��Ľ�������Ϊ��0��2������ô��x���ϵĽؾ�Ϊ-1����y���ϵĽؾ�Ϊ2��ͨ��
-�ɵøú�����ͼ���б��Ϊ2��
ͨ���Ķ��������ݣ�����������⣺
��1��д��һ�κ���y=-2x-3��������Ľ��㣻
��x��Ľ��������ǣ�
��y��Ľ��������ǣ�
��0��-3��
��0��-3��
��2��д��һ�κ���y=-2x-3���������ϵĽؾࣻ
��x���ϵĽؾ���
��y���ϵĽؾ���
-3
-3
��3�������ͼ���б�ʣ�
��4��ֱ��д��һ�κ���y=3x+5��ͼ���б����
3
3
��




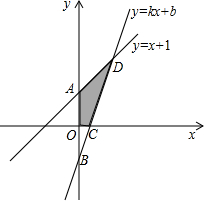 x���Լ�y=x+1��ͼ��ֱ��ڵ�C��D��
x���Լ�y=x+1��ͼ��ֱ��ڵ�C��D�� һ�κ���y=kx+b�뷴��������y=
һ�κ���y=kx+b�뷴��������y= ��2013•Ϋ������ͼ��������y=ax2+bx+c����ֱ��x=1�Գƣ��������ύ��A��B��C���㣬��AB=4����D��2��
��2013•Ϋ������ͼ��������y=ax2+bx+c����ֱ��x=1�Գƣ��������ύ��A��B��C���㣬��AB=4����D��2��