
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
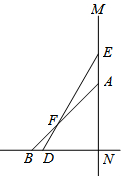 如图,一根6米长的竹竿DE斜靠的竖直的墙MN上,与地面所成的角∠EDN=60°,如果竹竿的顶端沿墙面下滑一段距离后竹竿与地面所成的角∠ABN=45°.
如图,一根6米长的竹竿DE斜靠的竖直的墙MN上,与地面所成的角∠EDN=60°,如果竹竿的顶端沿墙面下滑一段距离后竹竿与地面所成的角∠ABN=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
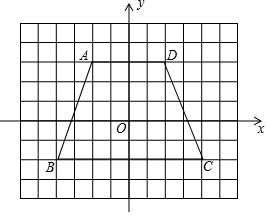 (1)写出如图所示的四边形ABCD各顶点的坐标.
(1)写出如图所示的四边形ABCD各顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲,乙两只昆虫一开始在数轴上的点A,点B处,它们在数轴上所对应的数分别为-8,4;这两只昆虫各自以一定的速度在数轴上运动,且甲昆虫的运动速度为2个单位/秒.
甲,乙两只昆虫一开始在数轴上的点A,点B处,它们在数轴上所对应的数分别为-8,4;这两只昆虫各自以一定的速度在数轴上运动,且甲昆虫的运动速度为2个单位/秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的差(单位:千克) | -2 | -1 | -1.5 | 0 | 1 | 1.5 |
| 筐数 | 2 | 5 | 3 | 10 | 4 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com