
【题目】如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.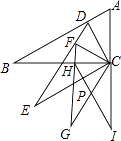
【答案】解:在Rt△ACB中,∠B=30°,∠ACB=90°,
∴∠A=90°﹣30°=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=30°,
在Rt△ACD中,AC=a,
∴AD= ![]() a,
a,
由勾股定理得:CD= ![]() =
= ![]() ,
,
同理得:FC= ![]() ×
× ![]() =
= ![]() ,CH=
,CH= ![]() ×
× ![]() =
= ![]() ,
,
在Rt△HCI中,∠I=30°,
∴HI=2HC= ![]() ,
,
由勾股定理得:CI= ![]() =
= ![]() ,
,
答:CI的长为 ![]() .
.
【解析】在Rt△ACD中,利用30度角的性质和勾股定理求CD的长;同理在Rt△ECD中求FC的长,在Rt△FCG中求CH的长;最后在Rt△HCI中,利用30度角的性质和勾股定理求CI的长.
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
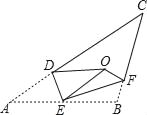
A. 40° B. 41° C. 42° D. 43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )

A.90° B.120° C.135° D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学活动小组为了调查居民的用水情况,从某社区的1500户家庭中随机抽取了30户家庭的月用水量,结果如下表所示:
月用水量(吨) | 3 | 4 | 5 | 7 | 8 | 9 | 10 |
户 数 | 4 | 3 | 5 | 11 | 4 | 2 | 1 |
(1)求这30户家庭月用水量的平均数,众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的办法引导人们节约用水,即规定每个家庭的月基本用水量为m(吨),家庭月用水量不超过m(吨)的部分按原价收费,超过m吨部分加倍收费,你认为上述问题中的平均数、众数、中位数中哪一个量作为月基本用水量比较合理?简述理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是某省2010年教育发展情况有关数据:
全省共有各级各类学校25000所,其中小学12500所,初中2000所,高中450所,其它学校10050所;全省共有在校学生995万人,其中小学440万人,初中200万人,高中75万人,其它280万人;全省共有在职教师48万人,其中小学20万人,初中12万人,高中5万人,其它11万人.
请将上述资料中的数据按下列步骤进行统计分析.
(1)整理数据:请设计一个统计表,将以上数据填入表格中.
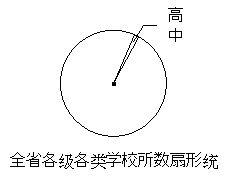
(2)描述数据:下图是描述全省各级各类学校所数的扇形统计图,请将它补充完整.
(3)分析数据:
①分析统计表中的相关数据,小学、初中、高中三个学段的师生比,最小的是哪个学段?请直接写出.(师生比=在职教师数︰在校学生数)
②根据统计表中的相关数据,你还能从其它角度分析得出什么结论吗?(写出一个即可)
③从扇形统计图中,你得出什么结论?(写出一个即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 甲、乙两名车工都加工要求尺寸是直径10毫米的零件.从他们所生产的零件中,各取5件,测得直径如下(单位:毫米)
甲:10.05, 10.02,9.97,9.95,10.01
乙:9.99,10.02,10.02,9.98,10.01
分别计算两组数据的标准差(精确到0.01),说明在尺寸符合规格方面,谁做得较好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com