Question

已知二次函数图象过点A（-2，3）、B（4，0）和坐标原点O．
（1）求该二次函数的解析式；
（2）若点C为该二次函数图象的顶点，那么四边形ABCO是什么特殊的四边形？请说明理由．

Answer 1

分析：（1）由二次函数图象过点A（-2，3）、B（4，0）和坐标原点O，即可设此二次函数的解析式为：y=ax²+bx，然后利用待定系数法即可求得该二次函数的解析式；
（2）由（1）即可得该二次函数图象的顶点C的坐标，然后利用待定系数法求得直线AB与直线OC的解析式，由系数相等，可得两直线平行，又由OA≠BC，可得四边形ABCO是梯形．

解答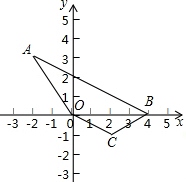：解：（1）∵二次函数图象过点A（-2，3）、B（4，0）和坐标原点O
∴设此二次函数的解析式为：y=ax²+bx，
∴

4a-2b=3 16a+4b=0

，
解得：

a= 1 4 b=-1

，
∴该二次函数的解析式为：y=

1

4

x²-x；

（2）∵y=

1

4

x²-x=

1

4

（x-2）²-1，
∴该二次函数图象的顶点C（2，-1），
设直线AB的解析式为：y=ax+b，
∴

-2a+b=3 4a+b=0

，
解得：

a=- 1 2 b=2

，
∴直线AB的解析式为：y=-

1

2

x+2，
设直线OC的解析式为：y=kx，
∴2k=-1，
∴k=-

1

2

，
∴直线OC的解析式为：y=-

1

2

x，
∵直线AB与直线OC的解析式一次项系数相等，
∴AB∥OC，
∵OA=

13

，BC=

5

，
∴四边形ABCO是梯形．

点评：此题考查了待定系数法求函数的解析式，一次函数平行的性质以及梯形的判定方法等知识．此题综合性较强，难度适中，解题的关键是方程思想与数形结合思想的应用．