Question

【题目】如图，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F，且FG⊥AB于G，FH⊥BC于H．

（1）求证：∠BEC=∠ADC；

（2）请你判断并FE与FD之间的数量关系，并证明.

Answer 1

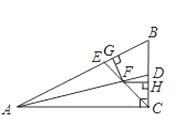
【答案】（1）证明见解析；（2）相等.

【解析】试题分析：（1）AD、CE分别是∠BAC、∠BCA的平分线，则可得∠DAC=∠DAB=15°

∠ACE= ∠ACB=45°，再由∠CDA=∠BAD+∠ABD，∠BEC=∠BAC+∠ECA，即可得；

（2）连接BF，根据角平分线的性质，可得FG=FH，又由在Rt△ABC中，∠ACB=90°，∠B=60°，求得∠GEF=75°=∠HDF，又由∠DHF=∠EHF=90°，利用AAS，即可证得△DHF≌△EGF，由全等三角形的对应边相等，即可证得FE=FD．

试题解析：(1)∵AD、CE分别是∠BAC、∠BCA的平分线，

∴∠DAC=∠DAB=∠BAC=15°

∠ACE=∠ACB=45°，

∴∠CDA=∠BAD+∠ABD=75°，∠BEC=∠BAC+∠ECA=75°，

∴∠BEC=∠ADC；

(2)相等，理由：如图，连接BF，

∵F是角平分线交点，

∴BF也是角平分线，

∴HF=FG，∠DHF=∠EGF=90°，

∵在Rt△ABC中，∠ACB=90°，∠ABC=60°，

∴∠BAC=30°，

∴∠DAC=12∠BAC=15°，

∴∠CDA=75°，

∵∠HFC=45°，∠HFG=120°，

∴∠GFE=15°，

∴∠GEF=75°=∠HDF，

在△DHF和△EGF中，

∠DHF=∠EGF，∠HDF=∠GEF，HF=GF，

∴△DHF≌△EGF(AAS)，

∴FE=FD.