
【题目】某中学形展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.

(1)根据图示填写下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | ||
九(2) | 85 | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.
【答案】(1)九(1)的平均数为85,众数为85,九(2)班的中位数是80;(2)九(1)班成绩好些,分析见解析;(3)![]() =70,
=70,![]() =100
=100
【解析】
(1)先根据条形统计图得出每个班5名选手的复赛成绩,然后平均数按照公式![]() ,中位数和众数按照概念即可得出答案;
,中位数和众数按照概念即可得出答案;
(2)对比平均数和中位数,平均数和中位数大的成绩较好;
(3)按照方差的计算公式![]() 计算即可.
计算即可.
解:(1)由图可知九(1)班5名选手的复赛成绩为:75、80、85、85、100,
九(2)班5名选手的复赛成绩为:70、100、100、75、80,
∴九(1)的平均数为(75+80+85+85+100)÷5=85,
九(1)的众数为85,
把九(2)的成绩按从小到大的顺序排列为:70、75、80、100、100,
∴九(2)班的中位数是80;
(2)九(1)班成绩好些.因为两个班平均分相同,但九(1)班的中位数高,所以九(1)班成绩好些.
(3)![]() =
=![]() =70
=70
![]() =
=![]() =100
=100


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
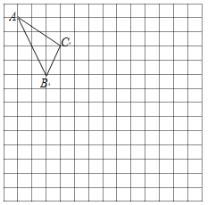
【题目】如图,在正方形网格中,每一个小正方形的边长为1.△ABC的三个顶点都在格点上,A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC向右平移6个单位的△A1B1C1,并写出C1的坐标 ;
(3)请画出△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
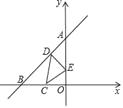
【题目】如图所示,直线 y=x+2 与两坐标轴分别交于A、B 两点,点 C 是 OB 的中点,D、E 分 别是直线 AB、y 轴上的动点,则△CDE 周长的最小值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC的中点,连结AD,在AD的延长线上取一点E,连结BE,CE.
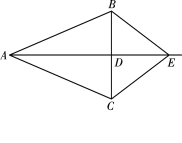
(1)求证:△ABE≌△ACE
(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴上,反比例函数y=![]() (k≠0,x>0)的图象与正方形的两边AB、BC分别交于点E、F,FD⊥x轴,垂足为D,连接OE、OF、EF,FD与OE相交于点G.下列结论:①OF=OE;②∠EOF=60°;③四边形AEGD与△FOG面积相等;④EF=CF+AE;⑤若∠EOF=45°,EF=4,则直线FE的函数解析式为
(k≠0,x>0)的图象与正方形的两边AB、BC分别交于点E、F,FD⊥x轴,垂足为D,连接OE、OF、EF,FD与OE相交于点G.下列结论:①OF=OE;②∠EOF=60°;③四边形AEGD与△FOG面积相等;④EF=CF+AE;⑤若∠EOF=45°,EF=4,则直线FE的函数解析式为![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
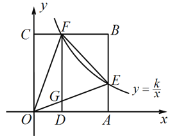
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
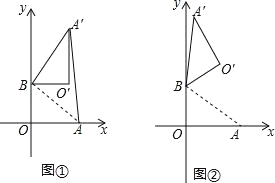
【题目】在平面直角坐标系中,O 为原点,点 A(4,0),点 B(0,3),把△ABO 绕点 B 逆时针旋转,得△A′BO′,点 A、O 旋转后的对应点为 A′、O′,记旋转角为ɑ.
(1)如图 1,若ɑ=90°,求 AA′的长;
(2)如图 2,若ɑ=120°,求点 O′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
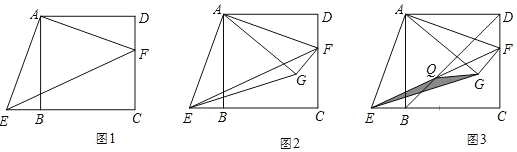
【题目】已知,在正方形 ABCD 中,AB=5,点 F 是边 DC 上的一个动点,将△ADF 绕点 A 顺时针旋转 90°至△ABE,点 F 的对应点 E 落在 CB 的延长线上,连接 EF.
(1)如图 1,求证:∠DAF+∠FEC=∠AEF;
(2)将△ADF 沿 AF 翻折至△AGF,连接 EG.
①如图 2,若 DF=2,求 EG 的长;
②如图 3,连接 BD 交 EF 于点 Q,连接 GQ,则 S△QEG 的最大值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com