Question

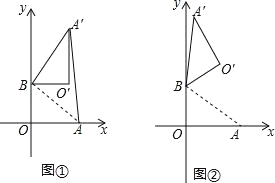
【题目】在平面直角坐标系中，O 为原点，点 A（4，0），点 B（0，3），把△ABO 绕点 B 逆时针旋转，得△A′BO′，点 A、O 旋转后的对应点为 A′、O′，记旋转角为ɑ．

(1)如图 1，若ɑ＝90°，求 AA′的长；

(2)如图 2，若ɑ＝120°，求点 O′的坐标．

Answer 1

【答案】（1）5；（2）点O′的坐标为（，）.

【解析】

（1）由题意可知OA=4，OB=3，由勾股定理求得AB=5.再由旋转的性质可得△ABA′为等腰直角三角形，即可得AA′=BA=5； （2）作O′H⊥y轴于点H，根据旋转的性质可得BO=BO′=3，∠OBO′=120°，即可得∠HBO′=60°.在Rt△BHO′中，∠BO′H′=30°，可得BH=BO′=.再由勾股定理求得O′H=.所以OH=OB+BH=，即可得点O′的坐标为（，）.

（1）∵点A（4，0），点B（0，3），

∴OA=4，OB=3.

∴AB==5.

∵△ABO绕点B逆时针旋转90°，得△A′BO′，

∴BA=BA′，∠ABA′=90°.

∴△ABA′为等腰直角三角形，

∴AA′=BA=5.

（2）作O′H⊥y轴于点H.

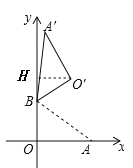
∵△ABO绕点B逆时针旋转120°，得△A′BO′，

∴BO=BO′=3，∠OBO′=120°.

∴∠HBO′=60°.

在Rt△BHO′中，∵∠BO′H=90°-∠HBO′=30°，

∴BH=BO′=.

∴O′H=.

∴OH=OB+BH=3+=.

∴点O′的坐标为（，）.