
 如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似? 分析 设经过t秒时,以△QBC与△ABC相似,则AP=2t,BP=8-2t,BQ=4t,利用两组对应边的比相等且夹角对应相等的两个三角形相似进行分类讨论:$\frac{BP}{BA}$=$\frac{BQ}{BC}$时,△BPQ∽△BAC,即$\frac{8-2t}{8}$=$\frac{4t}{16}$;当$\frac{BP}{BC}$=$\frac{BQ}{BA}$时,△BPQ∽△BCA,即$\frac{8-2t}{16}$=$\frac{4t}{8}$,然后方程解方程即可.
解答 解:设经过t秒时,以△QBC与△ABC相似,则AP=2t,BP=8-2t,BQ=4t,
∵∠PBQ=∠ABC,
∴当$\frac{BP}{BA}$=$\frac{BQ}{BC}$时,△BPQ∽△BAC,即$\frac{8-2t}{8}$=$\frac{4t}{16}$,解得t=2(s);
当$\frac{BP}{BC}$=$\frac{BQ}{BA}$时,△BPQ∽△BCA,即$\frac{8-2t}{16}$=$\frac{4t}{8}$,解得t=0.8(s);
即经过2秒或0.8秒时,△QBC与△ABC相似.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.利用时间表示相应线段长和利用相似比列方程是解决此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
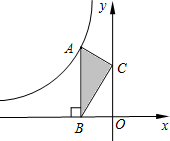 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<0 | |
| B. | b2-4ac的值可能为0 | |
| C. | 方程ax2+bx+c=0必有一根x0满足x1<x0<x2 | |
| D. | y1<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
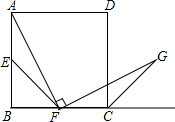 如图,在正方形ABCD中,点E、F分别是边AB、BC的中点,∠AFG=90°,且FG交正方形的外角∠DCP的平分线CG于点G.
如图,在正方形ABCD中,点E、F分别是边AB、BC的中点,∠AFG=90°,且FG交正方形的外角∠DCP的平分线CG于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x+1}{2}-1≥x②}\end{array}\right.$
解不等式组:$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x+1}{2}-1≥x②}\end{array}\right.$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com