Question

1．问题：如图1，正△ABC中，点D在边BC上（不与点B、C重合），求证：BD+DC＞AD．
思路：把△ACD绕点A顺时针旋转60°得到△ABE，连接ED．则有△ACD≌△ABE，DC=EB．
∵AD=AE，∠DAE=60°，
∴△ADE是等边三角形，
∴AD=DE．
在△DBE中，BD+EB＞DE，即：BD+DC＞AD．
拓展：①如图3，Rt△ABC中，点D在底边BC上（不与点B、C重合）．
求证：BD+DC＞$\sqrt{2}$AD．
②将①中的点D移到△ABC外或内时，BD、DC和AD之间的数量关系成为BD+DC≥$\sqrt{2}$AD，则等式成立的条件是把△ABD旋转，使AB与AC重合，然后绕AC旋转．
应用：如图4，△ABC中，AB=AC，∠BAC=α，D是△ABC外一点，且∠BDC+∠BAC=180°，则BD、DC与AD之间的数量关系是BD+DC＜2AD．

Answer 1

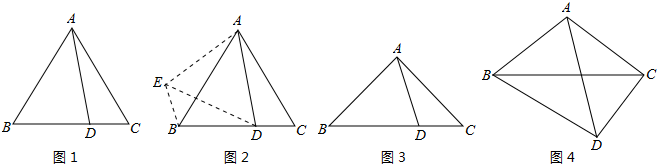
分析 ①把△ACD绕点A顺时针旋转90°得到△ABE，连接ED，则易证△ACD≌△ABE，根据勾股定理可以的到DE=$\sqrt{2}$AD，在△DBE中利用两边之和大于第三边即可得到；
②把△ACD绕点A顺时针旋转90°得到△ABE，连接ED，则易证△ACD≌△ABE，△AED是等腰直角三角形，则DE=$\sqrt{2}$AD，在△BED中，利用三角形三边关系定理即可证得；
应用：把△ACD绕点A顺时针旋转α，得到△ABE，则有△ACD≌△ABE，则易证E、B、D三点共线，在等腰△ADE中，利用两边之和大于第三边即可得到．

解答 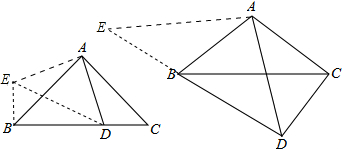解：①证明：把△ACD绕点A顺时针旋转90°得到△ABE，连接ED
则有△ACD≌△ABE，
DC=EB
∵AD=AE，∠DAE=90°
∴△ADE是等腰直角三角形
∴DE=$\sqrt{2}$AD
在△DBE中，BD+EB＞DE，
即：BD+DC＞$\sqrt{2}$AD；
②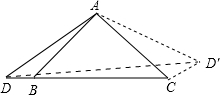把△ABD旋转，使AB与AC重合，然后绕AC旋转，得到△ACD′，
则BD=CD′，
在△CDD′中，CD+CD′＞DD′，
即BD+CD＞DD′，
∵△ADD′是钝角三角形，则DD′＞$\sqrt{2}$AD
当D运动到B的位置时，DD′=BC=$\sqrt{2}$AD．
∴BD+DC≥$\sqrt{2}$AD；
故答案为：把△ABD旋转，使AB与AC重合，然后绕AC旋转．
应用：猜想1：BD+DC＜2AD
证明：把△ACD绕点A顺时针旋转α，得到△ABE则有△ACD≌△ABE，DC=EB，∠ACD=∠ABE
∵∠BAC+∠BDC=180°
∴∠ABD+∠ACD=180°
∴∠ABD+∠ABE=180°
即：E、B、D三点共线．
∵AD=AE，
∴在△ADE中，AE+AD＞ED，即BD+DC＜2AD．
故答案为：BD+DC＜2AD

点评 本题考查了旋转的性质以及勾股定理，通过旋转构造全等的三角形，把所研究的三条线段转移到同一个三角形中，是解题的基本思路．