
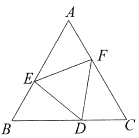
【题目】如图,点D,E,F分别在正三角形![]() 的三边上,且
的三边上,且![]() 也是正三角形.若
也是正三角形.若![]() 的边长为a,
的边长为a,![]() 的边长为b,则
的边长为b,则![]() 的内切圆半径为( )
的内切圆半径为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
证明△AEF≌△CFD≌△BDE,再求出AH=![]() (a-b),最后解直角三角形HAM,求出MH的长即可解决问题.
(a-b),最后解直角三角形HAM,求出MH的长即可解决问题.
如图,由于△ABC,△DEF都为正三角形,
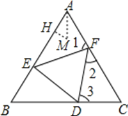
∴AB=BC=CA,EF=FD=DE,∠BAC=∠B=∠C=∠FED=∠EFD=∠EDF=60°,
∴∠1+∠2=∠2+∠3=120°,∠1=∠3;
在△AEF和△CFD中,
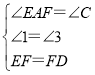 ,
,
∴△AEF≌△CFD(AAS);
同理可证:△AEF≌△CFD≌△BDE;
∴BE=AF,即AE+AF=AE+BE=a.
设M是△AEF的内心,MH⊥AE于H,
则AH=![]() (AE+AF-EF)=
(AE+AF-EF)=![]() (a-b);
(a-b);
∵MA平分∠BAC,
∴∠HAM=30°;
∴HM=AHtan30°=![]() (a-b)
(a-b)![]() =
=![]() (a-b)=
(a-b)=![]() .
.
故选:B.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】张阳把他和四位同学的年龄作为一组数据,计算出平均数是15,方差是0.4,则10年后张阳等5位同学的年龄的平均数和方差分别是( )
A.25和10.4B.15和4C.25和0.4D.15和0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(单位:m/s)与运动时间t (单位:s)的函数图象如图2,则该小球的运动路程y(单位:m)与运动时间t(单位:s)之间的函数图象大致是( )
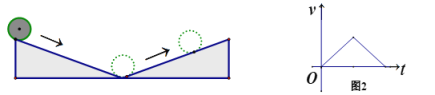
A.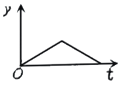 B.
B.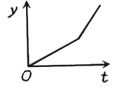 C.
C.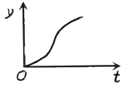 D.
D.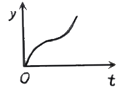
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前,玩具商店根据市场调查,用2500元购进一批儿童玩具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.第一、二批玩具每套的进价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.这本书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.用现代白话文可以这样理解:甲口袋中装有黄金9枚(每枚黄金重量相同),乙口袋中装有白银11枚(每枚白银重量相同),用称分别称这两个口袋的重量,它们的重量相等.若从甲口袋中拿出1枚黄金放入乙口袋中,乙口袋中拿出1枚白银放入甲口袋中,则甲口袋的重量比乙口袋的重量轻了13两(袋子重量忽略不计).问一枚黄金和一枚白银分别重多少两?请根据题意列方程(组)解之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王计划批发“山东大樱桃”和“泰国榴莲”两个品种的水果共120斤,樱桃和榴莲的批发价分别为32元/斤和40元/斤.设购买了樱桃x斤![]() .
.
(1)若小王批发这两种水果正好花费了4400元,那么小王分别购买了多少斤樱桃和榴莲?填写下表,并列方程求解;
品种 | 批发价(元) | 购买斤数 | 小王应付的钱数(元) |
樱桃 | 32 | x | |
榴莲 | 40 |
(2)设小王购买两种水果的总花费为y元,试写出y与x之间的函数表达式.
(3)若要求所批发的榴莲的斤数不少于樱桃斤数的2倍,那么购买樱桃的数量为多少时,可使小王的总花费最少?这个最少花费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
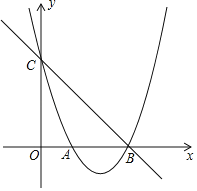
【题目】如图,已知二次函数y=ax2+bx+3的图象交x轴于点A(1,0),B(3,0),交y轴于点C.
(1)求这个二次函数的表达式;
(2)点P是直线BC下方抛物线上的一动点,求△BCP面积的最大值;
(3)直线x=m分别交直线BC和抛物线于点M,N,当△BMN是等腰三角形时,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按八折收费;在乙商场累计购物超过50元后,超出50元的部分按九折收费.设顾客累计购物![]() (单位:元),购物花费为
(单位:元),购物花费为![]() (单位:元).
(单位:元).
(1)分别写出在甲、乙两个商场购物时,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)顾客到哪家商场购物花费少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小寇随机调查了若干租用共享单车市民的骑车时间t(单位:分),将获得的据分成四组(A:0<t≤10,B:10<t≤20,C:20<t≤30, D:t>30),绘制了如下统计图,根据图中信息,解答下列问题:
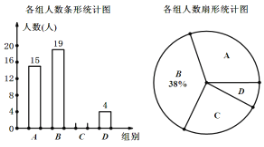
(1)小寇调查的总人数是 人;
(2)表示C组的扇形统计图的圆心角的度数是 °;
(3)如果小寇想从D组的甲、乙、丙、丁四人中随机选择两人进一步了解平时租用共享单车情况,请用列表或画树状图的方法求出丁被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com