
| A. | 2,4,2$\sqrt{3}$ | B. | 1,1,$\sqrt{2}$ | C. | 1,2,$\sqrt{5}$ | D. | $\sqrt{3}$,2,$\sqrt{5}$ |
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | $\sqrt{12}$ | C. | $\sqrt{{a}^{2}+4}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数1.230和1.23表示的意义相同 | |
| B. | 近似数79.0是精确到个位的数 | |
| C. | 将数60340精确到千位是6.0×104 | |
| D. | 近似数5千与近似数5000的精确度相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
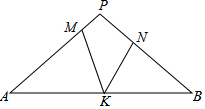 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )| A. | 44° | B. | 66° | C. | 96° | D. | 92° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
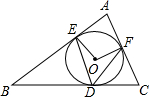 如图,⊙O内切于△ABC,切点分别为D、E、F,已知∠B=45°,∠C=65°,连接OE、OF、DE、DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D、E、F,已知∠B=45°,∠C=65°,连接OE、OF、DE、DF,那么∠EDF等于( )| A. | 45° | B. | 50° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线a∥b,∠3=85°,求∠1、∠2的度数,根据下面的解答过程,填空或填写理由.
如图,直线a∥b,∠3=85°,求∠1、∠2的度数,根据下面的解答过程,填空或填写理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com