
 如图,海中有一个小岛B,它的周围14海里内有暗礁,在小岛正西方有一点A测得在北偏东60°,方向上有一灯塔C,灯塔C在小岛B北偏东15°方向上20海里处,渔船跟踪鱼群沿AC方向航行,每小时航行10$\sqrt{2}$海里.
如图,海中有一个小岛B,它的周围14海里内有暗礁,在小岛正西方有一点A测得在北偏东60°,方向上有一灯塔C,灯塔C在小岛B北偏东15°方向上20海里处,渔船跟踪鱼群沿AC方向航行,每小时航行10$\sqrt{2}$海里.分析 (1)作BH⊥AC于H,根据余弦的概念求出BH,比较即可判断;
(2)根据正切的概念求出AH,求出AC的长,根据渔船的速度计算即可.
解答 解:(1)渔船不改变航向继续航行,没有触礁危险.
作BH⊥AC于H,
由题意得,∠CAB=30°,∠ABC=105°,
则∠ABH=60°,∠HBC=45°,
∴BH=BC×cos∠HBC=10$\sqrt{2}$,
∵10$\sqrt{2}$>14,
∴渔船不改变航向继续航行,没有触礁危险;
(2)HC=BH=10$\sqrt{2}$,
AH=$\frac{BH}{tan∠CAB}$=10$\sqrt{6}$,
∴AC=AH+HC=10$\sqrt{2}$+10$\sqrt{6}$,
则渔船从A点处航行到灯塔C,需要的时间为:(10$\sqrt{2}$+10$\sqrt{6}$)÷10$\sqrt{2}$=1+$\sqrt{3}$,
答:渔船从A点处航行到灯塔C,需要(1$+\sqrt{3}$)小时.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的定义是解题的关键.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
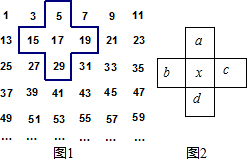 如图,将连续的奇数1,3,5,7,…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
如图,将连续的奇数1,3,5,7,…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,内错角相等 | |
| C. | 若两条直线都和第三条直线平行,则这两条直线平行 | |
| D. | 若两个角的和为180°,则这两个角互为邻补角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com