
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љx2+bx+cгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉКЭЕуBЃЌгыyжсНЛгкCЃЈ0ЃЌ3ЃЉЃЌжБЯпy=![]() +mОЙ§ЕуCЃЌгыХзЮяЯпЕФСэвЛНЛЕуЮЊЕуDЃЌЕуPЪЧжБЯпCDЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPFЁЭxжсгкЕуFЃЌНЛжБЯпCDгкЕуEЃЌЩшЕуPЕФКсзјБъЮЊmЃЎ
+mОЙ§ЕуCЃЌгыХзЮяЯпЕФСэвЛНЛЕуЮЊЕуDЃЌЕуPЪЧжБЯпCDЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPFЁЭxжсгкЕуFЃЌНЛжБЯпCDгкЕуEЃЌЩшЕуPЕФКсзјБъЮЊmЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНВЂЧѓГіЕуDЕФзјБъЃЛ
ЃЈ2ЃЉСЌНгPDЃЌЁїCDPЕФУцЛ§ЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧыЧѓГіУцЛ§ЕФзюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЁїCPEЪЧЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіmЕФжЕЃЎ

ЁОД№АИЁПЃЈ1ЃЉy=Љx2+2x+3ЃЌDЕузјБъЮЊЃЈ![]() ЃЉЃЛЃЈ2ЃЉЕБm=
ЃЉЃЛЃЈ2ЃЉЕБm=![]() ЪБЃЌЁїCDPЕФУцЛ§ДцдкзюДѓжЕЃЌзюДѓжЕЮЊ
ЪБЃЌЁїCDPЕФУцЛ§ДцдкзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉmЕФжЕЮЊ
ЃЛЃЈ3ЃЉmЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпНтЮіЪНКЭжБЯпCDЕФНтЮіЪНЃЌШЛКѓНтЗНГЬзщ ЕУDЕузјБъЃЛ
ЕУDЕузјБъЃЛ
ЃЈ2ЃЉЩшPЃЈmЃЌ-m2+2m+3ЃЉЃЌдђEЃЈmЃЌ-![]() m+3ЃЉЃЌдђPE=-m2+
m+3ЃЉЃЌдђPE=-m2+![]() mЃЌРћгУШ§НЧаЮУцЛ§ЙЋЪНЕУЕНSЁїPCD=
mЃЌРћгУШ§НЧаЮУцЛ§ЙЋЪНЕУЕНSЁїPCD=![]() ЁС
ЁС![]() ЁСЃЈ-m2+
ЁСЃЈ-m2+![]() mЃЉ=-
mЃЉ=-![]() m2+
m2+![]() mЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
mЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЬжТлЃКЕБPC=PEЪБЃЌm2+ЃЈ-m2+2m+3-3ЃЉ2=ЃЈ-m2+![]() mЃЉ2ЃЛЕБCP=CEЪБЃЌm2+ЃЈ-m2+2m+3-3ЃЉ2=m2+ЃЈ-
mЃЉ2ЃЛЕБCP=CEЪБЃЌm2+ЃЈ-m2+2m+3-3ЃЉ2=m2+ЃЈ-![]() m+3-3ЃЉ2ЃЛЕБEC=EPЪБЃЌm2+ЃЈ-
m+3-3ЃЉ2ЃЛЕБEC=EPЪБЃЌm2+ЃЈ-![]() m+3-3ЃЉ2=ЃЈ-m2+
m+3-3ЃЉ2=ЃЈ-m2+![]() mЃЉ2ЃЌШЛКѓЗжБ№НтЗНГЬМДПЩЕУЕНТњзуЬѕМўЕФmЕФжЕЃЎ
mЃЉ2ЃЌШЛКѓЗжБ№НтЗНГЬМДПЩЕУЕНТњзуЬѕМўЕФmЕФжЕЃЎ
ЃЈ1ЃЉАбAЃЈЉ1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉЗжБ№ДњШыy=Љx2+bx+cЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2+2x+3ЃЛ
АбCЃЈ0ЃЌ3ЃЉДњШыy=Љ![]() x+nЃЌНтЕУn=3ЃЌ
x+nЃЌНтЕУn=3ЃЌ
ЁржБЯпCDЕФНтЮіЪНЮЊy=Љ![]() x+3ЃЌ
x+3ЃЌ
НтЗНГЬзщ ЃЌНтЕУ
ЃЌНтЕУ![]()
Лђ![]() ЃЌ
ЃЌ
ЁрDЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉДцдкЃЎ
ЩшPЃЈmЃЌЉm2+2m+3ЃЉЃЌдђEЃЈmЃЌЉ![]() m+3ЃЉЃЌ
m+3ЃЉЃЌ
ЁрPE=Љm2+2m+3ЉЃЈЉ![]() m+3ЃЉ=Љm2+
m+3ЃЉ=Љm2+![]() mЃЌ
mЃЌ
ЁрSЁїPCD=![]()
![]() ЃЈЉm2+
ЃЈЉm2+![]() mЃЉ=Љ
mЃЉ=Љ![]() m2+
m2+![]() m=Љ
m=Љ![]() ЃЈmЉ
ЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЕБm=![]() ЪБЃЌЁїCDPЕФУцЛ§ДцдкзюДѓжЕЃЌзюДѓжЕЮЊ
ЪБЃЌЁїCDPЕФУцЛ§ДцдкзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБPC=PEЪБЃЌm2+ЃЈЉm2+2m+3Љ3ЃЉ2=ЃЈЉm2+![]() mЃЉ2ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=
mЃЉ2ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=![]() ЃЛ
ЃЛ
ЕБCP=CEЪБЃЌm2+ЃЈЉm2+2m+3Љ3ЃЉ2=m2+ЃЈЉ![]() m+3Љ3ЃЉ2ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=
m+3Љ3ЃЉ2ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=![]() ЃЈЩсШЅЃЉЛђm=
ЃЈЩсШЅЃЉЛђm=![]() ЃЛ
ЃЛ
ЕБEC=EPЪБЃЌm2+ЃЈЉ![]() m+3Љ3ЃЉ2=ЃЈЉm2+
m+3Љ3ЃЉ2=ЃЈЉm2+![]() mЃЉ2ЃЌНтЕУm=
mЃЉ2ЃЌНтЕУm=![]() ЃЈЩсШЅЃЉЛђm=
ЃЈЩсШЅЃЉЛђm=![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌmЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌдке§ЗНаЮABCDжаЃЌEЪЧABЩЯвЛЕуЃЌFЪЧADбгГЄЯпЩЯвЛЕуЃЌЧвDFЃНBEЃЎЧѓжЄЃКCEЃНCFЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдке§ЗНаЮABCDжаЃЌEЪЧABЩЯвЛЕуЃЌGЪЧADЩЯвЛЕуЃЌШчЙћЁЯGCEЃН45ЁуЃЌЧыФуРћгУЃЈ1ЃЉЕФНсТлжЄУїЃКGEЃНBEЃЋGDЃЎ
ЃЈ3ЃЉдЫгУЃЈ1ЃЉЃЈ2ЃЉНтД№жаЫљЛ§РлЕФОбщКЭжЊЪЖЃЌЭъГЩЯТЬтЃК
ШчЭМ3ЃЌдкжБНЧЬнаЮABCDжаЃЌADЁЮBCЃЈBCЃОADЃЉЃЌЁЯBЃН90ЁуЃЌABЃНBCЃЌEЪЧABЩЯвЛЕуЃЌЧвЁЯDCEЃН45ЁуЃЌBEЃН4ЃЌDE="10," ЧѓжБНЧЬнаЮABCDЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() жсе§АыжсЩЯвЛЕуЃЌЧв
жсе§АыжсЩЯвЛЕуЃЌЧв![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() жсЩЯЮЛгкЕу
жсЩЯЮЛгкЕу![]() гвВрЕФвЛИіЖЏЕуЃЌЩшЕу
гвВрЕФвЛИіЖЏЕуЃЌЩшЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
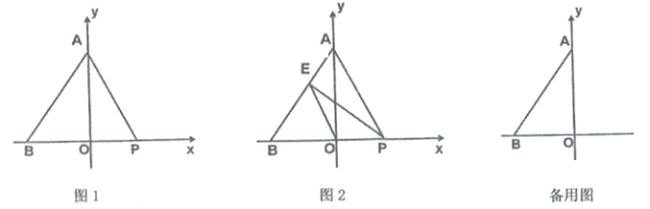
ЃЈ1ЃЉЕу![]() ЕФзјБъЮЊЃЈ ЃЉЃЛ
ЕФзјБъЮЊЃЈ ЃЉЃЛ
ЃЈ2ЃЉЕБ![]() ЪЧЕШбќШ§НЧаЮЪБЃЌЧѓ
ЪЧЕШбќШ§НЧаЮЪБЃЌЧѓ![]() ЕуЕФзјБъЃЛ
ЕуЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§Еу![]() зї
зї![]() НЛЯпЖЮ
НЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШєЕу
ЃЌШєЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦЕуЮЊ
ЕФЖдГЦЕуЮЊ![]() ЃЌЕБЕу
ЃЌЕБЕу![]() ЧЁКУТфдкжБЯп
ЧЁКУТфдкжБЯп![]() ЩЯЪБЃЌ
ЩЯЪБЃЌ![]() ЃЎЃЈжБНгаДГіД№АИЃЉ
ЃЎЃЈжБНгаДГіД№АИЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкОиаЮABCDжаЃЌЖЏЕуEДгAГіЗЂЃЌбиABЁњBCЗНЯђдЫЖЏЃЌЕБЕуEЕНДяЕуCЪБЭЃжЙдЫЖЏЃЌЙ§ЕуEзіFEЁЭAEЃЌНЛCDгкFЕуЃЌЩшЕуEдЫЖЏТЗГЬЮЊxЃЌFC=yЃЌШчЭМ2ЫљБэЪОЕФЪЧyгыxЕФКЏЪ§ЙиЯЕЕФДѓжТЭМЯѓЃЌЕБЕуEдкBCЩЯдЫЖЏЪБЃЌFCЕФзюДѓГЄЖШЪЧ![]() ЃЌдђОиаЮABCDЕФУцЛ§ЪЧ_____ЃЎ
ЃЌдђОиаЮABCDЕФУцЛ§ЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЩНЖЅНЈгавЛзљЬњЫўЃЌЫўИпBC=80УзЃЌВтСПШЫдБдквЛИіаЁЩНЦТЕФPДІВтЕУЫўЕФЕзВПBЕуЕФбіНЧЮЊ45ЁуЃЌЫўЖЅCЕуЕФбіНЧЮЊ60ЁуЃЎвбВтЕУаЁЩНЦТЕФЦТНЧЮЊ30ЁуЃЌЦТГЄMP=40УзЃЎЧѓЩНЕФИпЖШABЃЈОЋШЗЕН1УзЃЉЃЎЃЈВЮПМЪ§ОнЃК![]() Ёж1.414ЃЌ
Ёж1.414ЃЌ![]() Ёж1.732ЃЉ
Ёж1.732ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжа, ЁЯACB=90Ёу,ЕуDдкжБЯпBCЩЯ,BD=6,AD=BC,AC:CD=5:12,дђSЁїADB =_____.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌІЄP1OA1ЃЌІЄP2A1A2ЪЧЕШбќжБНЧШ§НЧаЮЃЌЕуP1ЁЂP2дкКЏЪ§y=![]() (x>0)ЕФЭМЯѓЩЯЃЌаББпOA1ЁЂA1A2ЖМдкxжсЩЯЃЌдђЕуA2ЕФзјБъЪЧ____________ЃЎ
(x>0)ЕФЭМЯѓЩЯЃЌаББпOA1ЁЂA1A2ЖМдкxжсЩЯЃЌдђЕуA2ЕФзјБъЪЧ____________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуDЃЌEЗжБ№дкACЃЌABЩЯЃЌBDгыCEЯрНЛгкЕуOЃЌвбжЊЁЯBЃНЁЯCЃЌЯжЬэМгЯТУцЕФФФвЛИіЬѕМўКѓЃЌШдВЛФмХаЖЈЁїABDЁеЁїACEЕФЪЧЃЈЁЁЁЁЃЉ
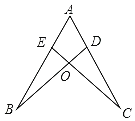
A.ADЃНAEB.ABЃНACC.BDЃНCED.ЁЯADBЃНЁЯAEC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌABЃНACЃЌЕуDдкБпBCЩЯЃЌЕуEдкБпACЩЯЃЌЧвADЃНAEЃЎ
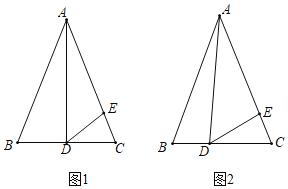
ЃЈ1ЃЉШчЭМ1ЃЌЕБADЪЧБпBCЩЯЕФИпЃЌЧвЁЯBADЃН30ЁуЪБЃЌЧѓЁЯEDCЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБADВЛЪЧБпBCЩЯЕФИпЪБЃЌЧыХаЖЯЁЯBADгыЁЯEDCжЎМфЕФЙиЯЕЃЌВЂМгвджЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com