练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在△ABC中, ∠ACB=90°,点D在直线BC上,BD=6,AD=BC,AC:CD=5:12,则S△ADB =_____.

    【答案】90或

    【解析】

    因为点D在直线BC上，所以两种情况应该考虑到：（1）点D在线段BC上；（2）点D在线段BC外.

    设AC＝5x，则CD＝12x，根据勾股定理得：AD＝13x，∵AD＝BC，∴BC＝13x，①点D在线段BC上时，BD＝BC－CD＝13x－12x＝x＝6，则AC＝30,CD＝72,BC＝78，∴S△ABD＝S△ABC－S△ACD＝ACBC－ACCD＝×30×78－×30×72＝90；②点D在线段BC外时，BD＝BC＋CD＝13x＋12x＝25x＝6，则x＝，∴AC＝，CD＝，AD＝BC＝，∴S△ABD＝BDAC＝×6×＝，故答案为或90.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，等腰直角三角形OAB的斜边AO在x轴上，，点B的坐标为．

    （1）求A点坐标；

    （2）过B作轴于C，点D从B出发沿射线BC以每秒2个单位的速度运动，连接AD、OD，动点D的运动时间为t，的面积为S，求S与t的数量关系，并直接写出t的取值范围；

    （3）在（2）的条件下，当点D运动到x轴下方时，延长AB交y轴于E，过E作于H，在x轴正半轴上取点F，连接BF交EH于G，，当时，求点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．

    （1）观察猜想

    如图1，当点D在线段BC上时，

    ①BC与CF的位置关系为：　 　．

    ②BC，CD，CF之间的数量关系为：　 　；（将结论直接写在横线上）

    （2）数学思考

    如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．

    （3）拓展延伸

    如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2，CD=BC，请求出GE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某服装店老板在武汉发现一款羽绒服，预测能畅销市场，就用a万元购进了x件.这款羽绒服面市后，果然十分畅销，很快售完.于是老板又在上海购进了同款羽绒服，所购数量比在武汉所购的数量多20%，单价贵20元，总进货款比前一次多23%.

    (1)请用含a和x的代数式分别表示在武汉以及上海购进的羽绒服的单价(单位:元/件);

    (2)若服装店老板两次进货共花费17.84万元，在销售这款羽绒服时每件定价都是 1200元，第二次销售后期由于天气转暖，服装还剩没有卖出，老板决定打8折销售，最后全部售完.两次销售，服装店老板共盈利多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0）和点B，与y轴交于C（0，3），直线y=+m经过点C，与抛物线的另一交点为点D，点P是直线CD上方抛物线上的一个动点，过点P作PF⊥x轴于点F，交直线CD于点E，设点P的横坐标为m．

    （1）求抛物线解析式并求出点D的坐标；

    （2）连接PD，△CDP的面积是否存在最大值？若存在，请求出面积的最大值；若不存在，请说明理由；

    （3）当△CPE是等腰三角形时，请直接写出m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

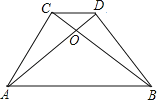
    【题目】如图，∠ADB＝∠ACB＝90°，AC与BD相交于点O，且OA＝OB，下列结论：①AD＝BC；②AC＝BD；③∠CDA＝∠DCB；④CD∥AB，其中正确的有（　　）

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E是平行四边形ABCD的边AD上的一动点(点E不与A、D重合)，连结CE并延长交BA的延长线于点F。

    (1) △CDE与△FAE是否总相似?为什么?

    (2)当E点为AD的中点时，求证：CE=EF;

    (3)当E点移至使EC⊥BC时，设AB=4cm，EF=6cm，∠D=60°时，求CB的长。(结果不取近似值)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知正方形的边长为，点，，，分别在正方形的四条边上，且，则四边形的形状为________，它的面积的最小值为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了预防“流感”，某学校对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量与时间成正比例，药物燃烧完后，与成反比例（如图所示）．现测得药物燃毕，此时室内空气中每立方米的含药量为．研究表明，当空气中每立方米的含药量不低于才有效，那么此次消毒的有效时间是（ ）

    A. 分钟 B. 分钟 C. 分钟 D. 分钟

    查看答案和解析>>

    同步练习册答案