
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 分别在正方形的四条边上,且
分别在正方形的四条边上,且![]() ,则四边形
,则四边形![]() 的形状为________,它的面积的最小值为________.
的形状为________,它的面积的最小值为________.

【答案】正方形![]()
【解析】
先证明△AEH≌△DFE≌△CGF≌△BHG,从而得到HE=EF=FG=HG,然后证明EFGH四边形有一个角是直角,从而可判断出四边形EFGH的形状,设AE=x,则AH=(![]() -x),依据正方形的面积公式以及勾股定理可得到四边形EFGH的面积与x的函数关系式,依据二次函数的性质求得二次函数的最小值即可.
-x),依据正方形的面积公式以及勾股定理可得到四边形EFGH的面积与x的函数关系式,依据二次函数的性质求得二次函数的最小值即可.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD, ∠A=∠B=∠C=∠D.
∵AE=DF=CG=BH,
∴AH=ED=FG=BG.
在△AEH、△DFE、△CGF、△BHG中, ,
,
∴△AEH≌△DFE≌CGF≌△BHG.
∴HE=EF=FG=HG.
∴四边形EFGH是菱形.
∵△AEH≌△DFE,
∴∠AEH=∠DFE.
∵∠AHE+∠AEH=90°,
∴∠DEF+∠AEH=90°.
∴∠HEF=90°.
∴EHGF为正方形.
设AE=x,则AH=(![]() -x).
-x).
∵正方形EFHG的面积=HE=AE+AH=x+(![]() -x) =2x-2
-x) =2x-2![]() x+5,
x+5,
∴当x=![]() 时,正方形的面积有最小值.
时,正方形的面积有最小值.
∴正方形EFHG的面积的最小值=![]() .
.
故答案为:正方形;![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.
(1)当CD=1时,求点E的坐标;
(2)如果设CD=t,梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在AC,AB上,BD与CE相交于点O,已知∠B=∠C,现添加下面的哪一个条件后,仍不能判定△ABD≌△ACE的是( )
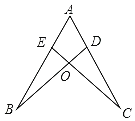
A.AD=AEB.AB=ACC.BD=CED.∠ADB=∠AEC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD=BE,∠D=∠E,∠ABC=∠DBE=90°,BF⊥AE,且点A,C,E在同一条直线上.
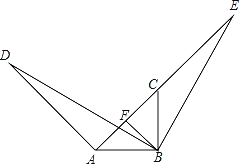
(1)求证:△DAB≌△ECB;
(2)若AD=3,AF=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,边长为
,边长为![]() 的正方形的一个顶点
的正方形的一个顶点![]() 在边
在边![]() 上,与
上,与![]() 另两边分
另两边分

别交于点![]() 、
、![]() ,
,![]() ,将正方形平移,使点
,将正方形平移,使点![]() 保持在
保持在![]() 上(
上(![]() 不与
不与![]() 重合),设
重合),设![]() ,正方形与
,正方形与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
![]() 求
求![]() 与
与![]() 的函数关系式并写出自变量
的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
![]() 为何值时
为何值时![]() 的值最大?
的值最大?
![]() 在哪个范围取值时
在哪个范围取值时![]() 的值随
的值随![]() 的增大而减小?
的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
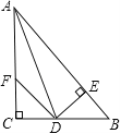
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,
(1)证明:CF=EB.
(2)证明:AB=AF+2EB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com