
【题目】如图,BD=BE,∠D=∠E,∠ABC=∠DBE=90°,BF⊥AE,且点A,C,E在同一条直线上.
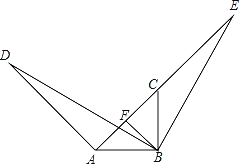
(1)求证:△DAB≌△ECB;
(2)若AD=3,AF=1,求BE的长.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=![]() ,把x=
,把x=![]() ,代入已知方程,
,代入已知方程,
得(![]() )2 +
)2 +![]() ﹣1=0.
﹣1=0.
化简,得y2+2y﹣4=0,
故所求方程为y2+2y﹣4=0
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)已知方程x2+2x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为 ;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
查看答案和解析>>
科目:初中数学 来源: 题型:
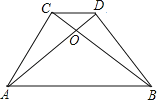
【题目】如图,∠ADB=∠ACB=90°,AC与BD相交于点O,且OA=OB,下列结论:①AD=BC;②AC=BD;③∠CDA=∠DCB;④CD∥AB,其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某地火车站及周围的简单平面图.(每个小正方形的边长代表1千米.)
(1)请以火车站所在的位置为坐标原点,建立平面直角坐标系,并表示出体育场A、超市B市场C、文化宫D的坐标.
(2)在这个坐标平面内,连接OA,若∠AOB的度数大约为53°,请利用所给数据描述体育场相对于火车站的位置.
(3)要想用第(2)问的方法描述文化宫在火车站的什么位置,需要测量哪些数据?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点![]() 是正比例函数
是正比例函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限的交点,
的图象在第一象限的交点,![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 的面积是2.
的面积是2.

(1)求![]() 的值以及这两个函数的解析式;
的值以及这两个函数的解析式;
(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() 是以
是以![]() 为腰的等腰三角形,求点
为腰的等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程:M:ax2+bx+c=0; N:cx2+bx+a=0,其中ac≠0,a≠c,以下四个结论:
①如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
②如果方程M有两根符号相同,那么方程N的两根符号也相同;
③如果m是方程M的一个根,那么![]() 是方程N的一个根;
是方程N的一个根;
④如果方程M和方程N有一个相同的根,那么这个根必是x=1
正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com