
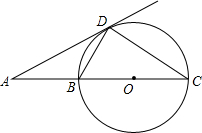
 如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 利用圆周角定理结合切线的性质得出∠BDC=∠ADO=90°,进而得出∠A,∠ADB的度数即可得出答案,再利用直角三角形中30°所对的边等于斜边的一半进而得出AB=$\frac{1}{2}$BC,判断即可.
解答 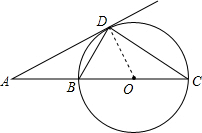 解:连接DO,
解:连接DO,
∵BC是⊙O的直径,AD是⊙O的切线,切点为D,
∴∠BDC=∠ADO=90°,
∵DO=CO,
∴∠C=∠CDO=30°,
∴∠A=30°,∠DBC=60°,
∠ADB=30°,
∴AD=DC,故①正确;
∵∠A=30°,∠DBC=60°,
∴∠ADB=30°,
∴AB=BD,故②正确;
∵∠C=30°,∠BDC=90°,
∴BD=$\frac{1}{2}$BC,
∵AB=BD,
∴AB=$\frac{1}{2}$BC,故③正确;
无法得到BD=CD,故④错误.
故选:B.
点评 此题主要考查了切线的性质以及圆周角定理和等腰三角形的性质等知识,得出∠A的度数是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (2,3)或(-2,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC互相垂直,如图所示.已知A与B之间的距离为20cm,若有两个小朋友在与点B相距10cm的点D处玩耍,玩累了他们分别沿不同的路线D→B→A,D→C→A到凉亭A处喝水休息,已知路线D→B→A与D→C→A路程相等,求AC的长度.
在某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC互相垂直,如图所示.已知A与B之间的距离为20cm,若有两个小朋友在与点B相距10cm的点D处玩耍,玩累了他们分别沿不同的路线D→B→A,D→C→A到凉亭A处喝水休息,已知路线D→B→A与D→C→A路程相等,求AC的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
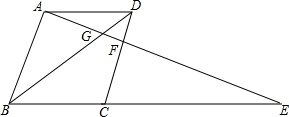 如图,在菱形ABCD的边BC的延长线上取点E,AE分别与CD与BD交于F和G,现在,有∠BGA:∠BAG=1:2,EF=21,FG=4,请求出菱形ABCD的边长.
如图,在菱形ABCD的边BC的延长线上取点E,AE分别与CD与BD交于F和G,现在,有∠BGA:∠BAG=1:2,EF=21,FG=4,请求出菱形ABCD的边长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com