
分析 由平方差公式可知:(x+y)(x-y)=7,得出x+y=±1或±7,对应x-y=±7或±1,由此分别列出方程组解答即可.
解答 解:∵x2-y2=7,
∴(x+y)(x-y)=7,
∵x、y是整数,
∴x+y=±1或±7,对应x-y=±7或±1,
则$\left\{\begin{array}{l}{x+y=7}\\{x-y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x+y=-7}\\{x-y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x+y=-1}\\{x-y=-7}\end{array}\right.$或$\left\{\begin{array}{l}{x+y=1}\\{x-y=7}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=-3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=-3}\end{array}\right.$;
∴xy=64或-$\frac{1}{64}$或-64或$\frac{1}{64}$.
故答案为:64或-$\frac{1}{64}$或-64或$\frac{1}{64}$.
点评 此题考查因式分解的实际运用,掌握平方差公式和分类讨论思想是解决问题的关键.


科目:初中数学 来源: 题型:解答题
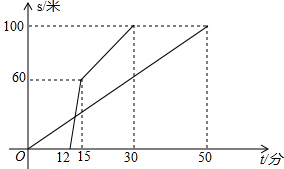 在“龟兔赛跑”中,兔子输给乌龟极不服气,所以它约乌龟再赛一场,以雪耻前辱.在这次赛跑中乌龟提高了速度,兔子也全力以赴.但兔子在跑步过程中腿受伤了,速度也由此减慢了,乌龟一直匀速跑到最后.如图是乌龟和兔子跑步的路程S(米)与乌龟出发的时间t(分)之间的函数图象.根据图象提供的信息解决问题:
在“龟兔赛跑”中,兔子输给乌龟极不服气,所以它约乌龟再赛一场,以雪耻前辱.在这次赛跑中乌龟提高了速度,兔子也全力以赴.但兔子在跑步过程中腿受伤了,速度也由此减慢了,乌龟一直匀速跑到最后.如图是乌龟和兔子跑步的路程S(米)与乌龟出发的时间t(分)之间的函数图象.根据图象提供的信息解决问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
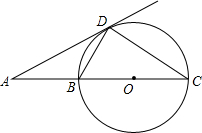 如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
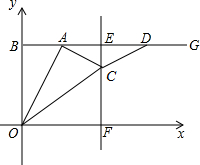 如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上一个动点(点A与点B不重合),在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C,连接OC、CD.设点A的横坐标为t.
如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上一个动点(点A与点B不重合),在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C,连接OC、CD.设点A的横坐标为t.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
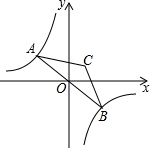 如图,点A是双曲线y=-$\frac{6}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为( )
如图,点A是双曲线y=-$\frac{6}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com