
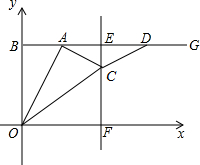
 如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上一个动点(点A与点B不重合),在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C,连接OC、CD.设点A的横坐标为t.
如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上一个动点(点A与点B不重合),在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C,连接OC、CD.设点A的横坐标为t.分析 (1)由点B坐标为(0,8),可知OB=8,根据线段垂直平分线的定义可知:AE=4,从而求得:BE=t+4,故此点E的坐标为(t+4,8);
(2)过点D作DH⊥OF,垂足为H.先证明△OBA∽△AEC,由相似三角形的性质可知$\frac{EC}{AB}=\frac{AE}{OB}$,可求得EC=$\frac{1}{2}t$,从而得到点C的坐标为(t+4,8-$\frac{1}{2}t$),因为∠OCD=180°,CF∥DH,可知$\frac{OF}{OH}=\frac{FC}{DH}$,即$\frac{t+4}{t+8}=\frac{8-\frac{1}{2}t}{8}$从而可解得t的值;
(3)三角形OCF的面积=$\frac{1}{2}×OF•FC$,从而可得S与t的函数关系式.
解答 解:(1)∵点B坐标为(0,8),
∴OB=8.
∵AD=OB,EF垂直平分AD,
∴AE=4.
∴BE=t+4.
∴点E的坐标为(t+4,8);
(2)如图所示;过点D作DH⊥OF,垂足为H.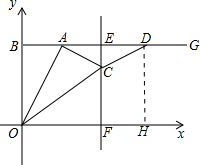
∵AC⊥OA,
∴∠OAC=90°.
∴∠BAO+∠EAC=90°.
又∵∠BOA+∠BAO=90°,
∴∠EAC=∠BOA.
又∵∠OBA=∠AEC,
∴△OBA∽△AEC.
∴$\frac{EC}{AB}=\frac{AE}{OB}$,即$\frac{EC}{t}=\frac{4}{8}$.
∴EC=$\frac{1}{2}t$.
∴点C的坐标为(t+4,8-$\frac{1}{2}t$)
∵∠OCD=180°,
∴点C在OD上.
∵CF∥DH,
∴$\frac{OF}{OH}=\frac{FC}{DH}$,即$\frac{t+4}{t+8}=\frac{8-\frac{1}{2}t}{8}$
解得:${t}_{1}=4\sqrt{5}-4$,${t}_{2}=-4\sqrt{5}-4$(舍去).
所以当t=4$\sqrt{5}$-4时,∠OCD=180°.
(3)当0<t<16时,三角形OCF的面积=$\frac{1}{2}$×OF•FC=$\frac{1}{2}×$(t+4)(8$-\frac{1}{2}$t)=$-\frac{1}{4}{t}^{2}+3t+16$,
当t>16时,三角形OCF的面积=$\frac{1}{2}$×OF•FC=$\frac{1}{2}×$(t+4)($\frac{1}{2}$t-8)=$\frac{1}{4}{t}^{2}-3t-16$,
∴s与t的函数关系式为s=$\left\{\begin{array}{l}{-\frac{1}{4}{t}^{2}+3t+16(0<t<16)}\\{\frac{1}{4}{t}^{2}-3t-16(t>16)}\end{array}\right.$.
点评 本题主要考查的是相似三角形的性质和判定,用含字母t的式子表示点C的坐标是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 蔬菜种类 | 黄瓜 | 豆角 | 西红柿 |
| 每辆汽车运载量/吨 | 6 | 5 | 4 |
| 每吨所需运费/元/吨 | 120 | 160 | 180 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a-b+c<0,③2a=b,④4a+2b+c>0,⑤若点(-2,y1)和(-$\frac{1}{3}$,y2)在该图象上,则y1>y2.其中正确的结论是②④(填入正确结论的序号).
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a-b+c<0,③2a=b,④4a+2b+c>0,⑤若点(-2,y1)和(-$\frac{1}{3}$,y2)在该图象上,则y1>y2.其中正确的结论是②④(填入正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
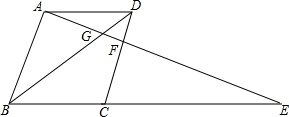 如图,在菱形ABCD的边BC的延长线上取点E,AE分别与CD与BD交于F和G,现在,有∠BGA:∠BAG=1:2,EF=21,FG=4,请求出菱形ABCD的边长.
如图,在菱形ABCD的边BC的延长线上取点E,AE分别与CD与BD交于F和G,现在,有∠BGA:∠BAG=1:2,EF=21,FG=4,请求出菱形ABCD的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com