
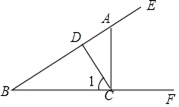
【题目】如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有_____.
【答案】①④
【解析】
根据垂直定义可得∠BCA=90°,∠ADC=∠BDC=∠ACF=90°,然后再根据余角定义和补角定义进行分析即可.
∵AC⊥BF,∴∠BCA=90°,∴∠ACD+∠1=90°,∴∠1是∠ACD的余角,故①正确;
∵CD⊥BE,∴∠ADC=∠CDB=90°,∴∠B+∠BCD=90°,∠ACD+∠DAC=90°.
∵∠BCA=90°,∴∠B+∠BAC=90°,∠1+∠ACD=90°,∴图中互余的角共有4对,故②错误;
∵∠1+∠DCF=180°,∴∠1的补角是∠DCF.
∵∠1+∠DCA=90°,∠DAC+∠DCA=90°,∴∠1=∠DAC.
∵∠DAC+∠CAE=180°,∴∠1+∠CAE=180°,∴∠1的补角有∠CAE,故③说法错误;
∵∠ACB=90°,∠ACF=90°,∠ADC=∠BDC=90°,∴∠BDC,∠ACB,∠ACF和∠ADC互补,故④说法正确.
正确的是①④.
故答案为:①④.


科目:初中数学 来源: 题型:
【题目】如图,已知AB是O的直径,点C在O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.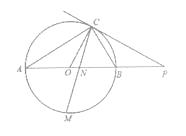
(1)求证:PC是O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
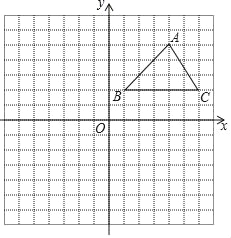
【题目】我们规定,在平面直角坐标系中,将一个图形先关于y轴对称,再向下平移2个单位记为1次“R变换”.
(1)画出△ABC经过1次“R变换”后的图形△A1B1C1;
(2)若△ABC经过3次“R变换”后的图形为△A3B3C3,则顶点A3坐标为 ;
(3)记点P(a,b)经过n次“R变换”后的点为Pn,直接写出Pn的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有学生55人,其中男生与女生的人数之比为6:5.
(1)求出该班男生与女生的人数;
(2)学校要从该班选出20人参加学校的合唱团,要求:①男生人数不少于7人;②女生人数超过男生人数2人以上.请问男、女生人数有几种选择方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年5月22日﹣29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛.在比赛中,某次羽毛球的运动路线可以看作是抛物线y=﹣ ![]() x2+bx+c的一部分(如图),其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,那么这条抛物线的解析式是( )
x2+bx+c的一部分(如图),其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,那么这条抛物线的解析式是( ) 
A.y=﹣ ![]() x2+
x2+ ![]() x+1
x+1
B.y=﹣ ![]() x2+
x2+ ![]() x﹣1
x﹣1
C.y=﹣ ![]() x2﹣
x2﹣ ![]() x+1
x+1
D.y=﹣ ![]() x2﹣
x2﹣ ![]() x﹣1
x﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,你能求出楼房AB的高度吗?(tan54°≈1.38,结果精确到0.1m)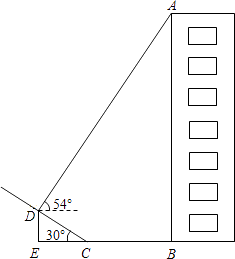
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,半圆O的直径DE=12cm,点E与点C重合,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在BC所在的直线上.设运动时间为x(s),半圆O在△ABC的重叠部分的面积为S(cm2). 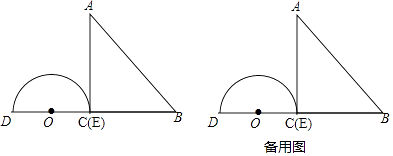
(1)当x=(s)时,点O与线段BC的中点重合;
(2)在(1)的条件下,求半圆O与△ABC的重叠部分的面积S;
(3)当x为何值时,半圆O所在的圆与△ABC的边所在的直线相切?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com