
【题目】如图,已知AB是O的直径,点C在O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.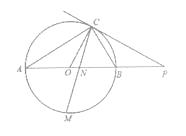
(1)求证:PC是O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
【答案】
(1)
证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)
证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= ![]() AB.
AB.
(3)
解:连接MA,MB,
∵点M是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴ ![]() ,
,
∴BM2=MNMC.
又∵AB是⊙O的直径, ![]() =
= ![]() ,
,
∴∠AMB=90°,AM=BM.
∵AB=4,
∴BM=2 ![]() .
.
∴MNMC=BM2=8.
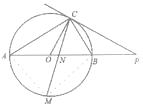
【解析】(1)由半径OA=OC,可得等边对等角∠A=∠ACO,则∠COB=2∠A,已知∠COB=2∠PCB,∠A=∠ACO=∠PCB.由直径所对的圆周角是直角可得∠ACO+∠OCB=90°.从而转换得到∠PCB+∠OCB=90°即可证得;(2)“等角对等边”与“等边对等角”相互运用可证OC=BC;(3)连接MA,MB,先证明△MBN∽△MCB.则 ![]() ,即BM2=MNMC.由AB是⊙O的直径,
,即BM2=MNMC.由AB是⊙O的直径, ![]() =
= ![]() ,AB=4,解出BM,从而可解得MNMC.
,AB=4,解出BM,从而可解得MNMC.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠A=∠B=30°,CD平分∠ACB,M、N分别是BC、AC的中点.图中等于60°的角有( )个.
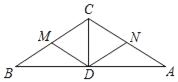
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知含字母x,y的多项式是:3[x2+2(y2+xy﹣2)]﹣3(x2+2y2)﹣4(xy﹣x﹣1)
(1)化简此多项式;
(2)小红取x,y互为倒数的一对数值代入化简的多项式中,恰好计算得多项式的值等于0,那么小红所取的字母y的值等于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上, ![]() =
= ![]() ,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=
,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y= ![]() 的图象过点C,若以CD为边的正方形的面积等于
的图象过点C,若以CD为边的正方形的面积等于 ![]() ,则k的值是.
,则k的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为25和17,则△EDF的面积为( )

A. 4 B. 5 C. 5.5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上有A、B两点,A在B的左侧,已知点B对应的数为2,点A对应的数为a.
(1)若a=﹣3,则线段AB的长为 (直接写出结果);
(2)若点C在线段AB之间,且AC﹣BC=2,求点C表示的数(用含a的式子表示);
(3)在(2)的条件下,点D是数轴上A点左侧一点,当AC=2AD,BD=4BC,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有_____.
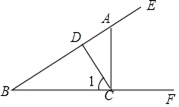
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com