
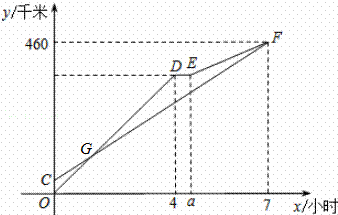
甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
请结合图象信息解答下列问题:
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x的函数关系式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时与甲车相距15千米?直接写出答案.
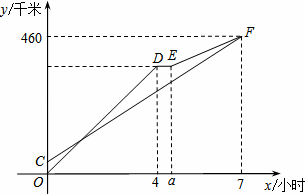
解:(1)a=4.5,
甲车的速度=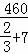 =60(千米/小时);
=60(千米/小时);
(2)设乙开始的速度为v千米/小时,
则4v+(7﹣4.5)(v﹣50)=460,解得v=90(千米/小时),
4v=360,
则D(4,360),E(4.5,360),
设直线EF的解析式为y=kx+b,
把E(4.5,360),F(7,460)代入得 ,
,
解得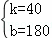 .
.
所以线段EF所表示的y与x的函数关系式为y=40x+180(4.5≤x≤7);
(3)甲车前40分钟的路程为60× =40千米,则C(0,40),
=40千米,则C(0,40),
设直线CF的解析式为y=mx+n,
把C(0,40),F(7,460)代入得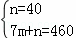 ,解得
,解得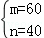 ,
,
所以直线CF的解析式为y=60x+40,
易得直线OD的解析式为y=90x(0≤x≤4),
设甲乙两车中途相遇点为G,由60x+40=90x,解得x=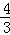 小时,即乙车出发
小时,即乙车出发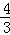 小时后,甲乙两车相遇,
小时后,甲乙两车相遇,
当乙车在CG段时,由60x+40﹣90x=15,解得x=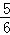 ,介于0~
,介于0~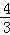 小时之间,符合题意;
小时之间,符合题意;
当乙车在GD段时,由90x﹣(60x+40)=15,解得x=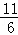 ,介于
,介于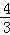 ~4小时之间,符合题意;
~4小时之间,符合题意;
当乙车在DE段时,由360﹣(60x+40)=15,解得x=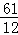 ,不介于4~4.5之间,不符合题意;
,不介于4~4.5之间,不符合题意;
当乙车在EF段时,由40x+180﹣(60x+40)=15,解得x=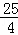 ,介于4.5~7之间,符合题意.
,介于4.5~7之间,符合题意.
所以乙车出发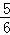 小时或
小时或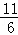 小时或
小时或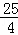 小时,乙与甲车相距15千米.
小时,乙与甲车相距15千米.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,矩形OA BC的对角线OB,AC相交于点D,BE∥AC,AE∥OB.
BC的对角线OB,AC相交于点D,BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:解答题
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
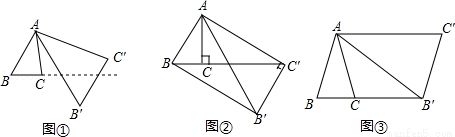
(1)如图①,对△ABC作变换[50°,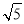 ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:选择题
下列运算正确的是( )
A.2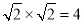 B.2a3a4=2a12 C.(2a4)3=8a7 D.a8÷a2=a4
B.2a3a4=2a12 C.(2a4)3=8a7 D.a8÷a2=a4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市锡山区九年级上学期期末考试数学试卷(解析版) 题型:填空题
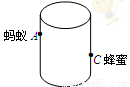
如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为_________________cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com