

���� ��1������ţA���ٶ�Ϊx��λ����/�룬��ţB���ٶ�Ϊ4x��λ����/�룬��������ţ���15����λ�г�������⼴�ɣ�
��2�������෴���Ķ��壬��ţA��B��ԭ��ľ�����ȣ��ֱ��ʾ����ţA��B����Ӧ�����ľ���ֵ��Ȼ���г�������⼴�ɣ�
��3����y�����ţB����ţA��������ţB����ţA��·�̶�15�г����̣����õ�ʱ�䣬�ٸ���·��=�ٶȡ�ʱ����м��㼴�ɵý⣮
��� �⣺��1������ţA���ٶ�Ϊx��λ����/�룬��ţB���ٶ�Ϊ4x��λ����/�룬
�������⣬3$\sqrt{2}$��x+4x��=15��
��ã�x=$\frac{\sqrt{2}}{2}$��
������ţA���ٶ�Ϊ$\frac{\sqrt{2}}{2}$��λ����/�룬��ţB���ٶ�Ϊ2$\sqrt{2}$��λ����/�룬
3$\sqrt{2}$��ʱ����ţA��λ����-$\frac{3}{2}\sqrt{2}$����ţB��λ����6$\sqrt{2}$��
��ͼ1�ϱ�ע���£�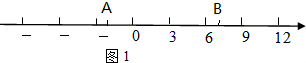
��2����x��ʱԭ��ǡ�ô���������ţ�����м䣬
������ã�6$\sqrt{2}$-4x=$\frac{3}{2}\sqrt{2}$+x��
��ã�x=$\frac{9}{10}\sqrt{2}$��
��3����y�����ţB����ţA��
������ã�2$\sqrt{2}$y-$\frac{\sqrt{2}}{2}$y=15��
��ã�y=5$\sqrt{2}$��
5$\sqrt{2}$��2$\sqrt{5}$=10$\sqrt{10}$��
��C�ӿ�ʼ�˶���ֹͣ�˶�����ʻ��·����10$\sqrt{10}$����λ���ȣ�
���� ���⿼����һԪһ�η��̵�Ӧ�ã�����ؼ���Ҫ������Ŀ����˼��������Ŀ�������������ҳ����ʵĵ�����ϵ�г����̣�����⣮


 ��������ѧ����ϵ�д�
��������ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ƽ���ı��� | B�� | ���� | C�� | ���� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
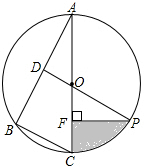 ��ͼ����֪��O�ǡ�ABC�����Բ��AC��ֱ������A=30�㣬BC=2����D��AB���е㣬����DO���ӳ�����O�ڵ�P������P��PF��AC�ڵ�F��
��ͼ����֪��O�ǡ�ABC�����Բ��AC��ֱ������A=30�㣬BC=2����D��AB���е㣬����DO���ӳ�����O�ڵ�P������P��PF��AC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
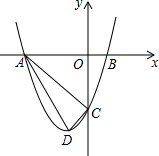 ���κ���y=ax2+bx+c��a��0����ͼ����x�ύ��A��-3��0����B��1��0�����㣬��y�ύ�ڵ�C��0��-3m��������m��0��������ΪD��
���κ���y=ax2+bx+c��a��0����ͼ����x�ύ��A��-3��0����B��1��0�����㣬��y�ύ�ڵ�C��0��-3m��������m��0��������ΪD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com