
【题目】如图,在平面直角坐标系中2条直线,分别为![]()
![]() ,
,![]()
![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,抛物线
,抛物线![]() 过
过![]() 、
、![]() 、
、![]() 三点.
三点.
下列判断中:
①![]() ;
;
②抛物线关于直线![]() 轴对称 ;
轴对称 ;
③点![]() 在抛物线上方;
在抛物线上方;
④![]() ;
;
⑤![]() .其中正确的个数有( )
.其中正确的个数有( )
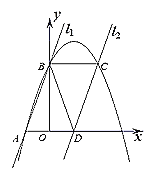
A.5B.4C.3D.2
【答案】C
【解析】
根据直线l1的解析式求出A(-1,0),B(0,3),根据平行于x轴的直线上任意两点纵坐标相同得出C点纵坐标与B点纵坐标相同都是3,再根据二次函数图象上点的坐标特征求出C(2,3).利用待定系数法求出抛物线的解析式为![]() ,进而判断各选项即可.
,进而判断各选项即可.
∵直线l1:y=3x+3交x轴于点A,交y轴于点B,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
∴A(-1,0),B(0,3),
∵直线l2:y=3x-3交x轴于点D,过点B作x轴的平行线交l2于点C,
令![]() ,则
,则![]() ,
,
∴D(1,0),
∵C点纵坐标与B点纵坐标相同都是3,
把y=3代入y=3x-3,
解得x=2,
∴C(2,3),
∵抛物线y=ax2+bx+c过A、B、C三点,
∴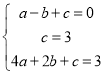
解得: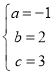
∴抛物线的解析式为![]() ,
,
①当x=1时,![]() ,
,
∴当x=1时,![]()
![]() ,故①错误;
,故①错误;
②∵![]() ,
,
∴抛物线的对称轴是直线![]() ,
,
∴抛物线关于直线x=1对称,故②正确;
③∵抛物线的对称轴是直线![]() ,
,
∴抛物线顶点坐标为:(1,4),
∵![]() ,
,
∴点![]() 即为(1,3),
即为(1,3),
∴点![]() 在在抛物线下方,故③错误;
在在抛物线下方,故③错误;
④∵直线BC∥![]() 轴,且B(0,3),C(2,3),
轴,且B(0,3),C(2,3),
∴BC=2,
∴![]() ,故④正确;
,故④正确;
⑤∵![]() ,
,
∴![]() ,故⑤正确;
,故⑤正确;
综上:②④⑤正确,共3个,
故选:C.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
(1)求抛物线的解析式和顶点坐标;
(2)将该抛物线向左平移 个单位长度后,可使平移后的抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式: ;
(3)观察图象,写出关于x的不等式ax2+bx+c+3>0的解集 .
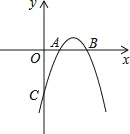
查看答案和解析>>
科目:初中数学 来源: 题型:
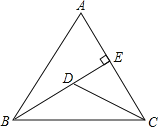
【题目】如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+![]() BD的最小值是( )
BD的最小值是( )
A.2![]() B.4
B.4![]() C.5
C.5![]() D.10
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
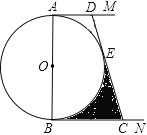
【题目】如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE.
(1)求证:DA=DE;
(2)若AB=6,CD=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
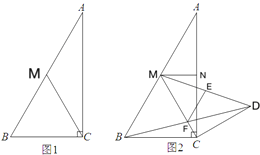
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点M是AB边的中点.
(1)如图1,若CM=![]() ,求△ACB的周长;
,求△ACB的周长;
(2)如图2,若N为AC的中点,将线段CN以C为旋转中心顺时针旋转60°,使点N至点D处,连接BD交CM于点F,连接MD,取MD的中点E,连接EF.求证:3EF=2MF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】空间任意选定一点![]() ,以点
,以点![]() 为端点,作三条互相垂直的射线
为端点,作三条互相垂直的射线![]() ,
,![]() ,
,![]() .这三条互相垂直的射线分别称作
.这三条互相垂直的射线分别称作![]() 轴、
轴、![]() 轴、
轴、![]() 轴,统称为坐标轴,它们的方向分别为
轴,统称为坐标轴,它们的方向分别为![]() (水平向前),
(水平向前),![]() (水平向右),
(水平向右),![]() (竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为
(竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为![]() ,
,![]() ,
,![]() ,且
,且![]() 的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体
的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
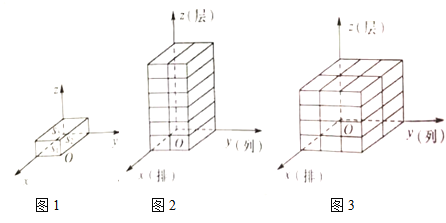
所在的面与![]() 轴垂直,如图1所示.若将
轴垂直,如图1所示.若将![]() 轴方向表示的量称为几何体码放的排数,
轴方向表示的量称为几何体码放的排数,![]() 轴方向表示的量称为几何体码放的列数,二轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了
轴方向表示的量称为几何体码放的列数,二轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作
层,用有序数组记作![]() ,如图3的几何体码放了
,如图3的几何体码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作
层,用有序数组记作![]() .这样我们就可用每一个有序数组
.这样我们就可用每一个有序数组![]() 表示一种几何体的码放方式.
表示一种几何体的码放方式.
(1)有序数组![]() 所对应的码放的几何体是______________;
所对应的码放的几何体是______________;
A.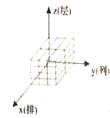 B.
B.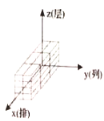 C.
C.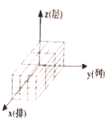 D.
D.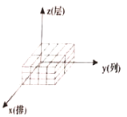
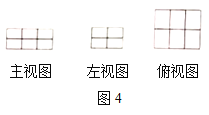
(2)图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为(______,_______,_______),组成这个几何体的单位长方体的个数为____________个.
(3)为了进一步探究有序数组![]() 的几何体的表面积公式
的几何体的表面积公式![]() ,某同学针对若干个单位长方体进行码放,制作了下列表格:
,某同学针对若干个单位长方体进行码放,制作了下列表格:
几何体有序数组 | 单位长方体的个数 | 表面上面积为S1的个数 | 表面上面积为S2的个数 | 表面上面积为S3的个数 | 表面积 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上规律,请直接写出有序数组![]() 的几何体表面积
的几何体表面积![]() 的计算公式;(用
的计算公式;(用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)
(4)当![]() ,
,![]() ,
,![]() 时,对由
时,对由![]() 个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对
个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对![]() 个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(______,_______, ______),此时求出的这个几何体表面积的大小为____________(缝隙不计)
个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(______,_______, ______),此时求出的这个几何体表面积的大小为____________(缝隙不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com