
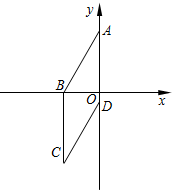
 如图,四边形ABCD为菱形,已知A(0,4),B(-3,0),点D在y轴上.求点D的坐标和对角线AC的长.
如图,四边形ABCD为菱形,已知A(0,4),B(-3,0),点D在y轴上.求点D的坐标和对角线AC的长. 分析 先利用勾股定理计算出AB=5,再利用菱形的性质得AD=BC=AB=5,BC∥AD,则可写出D(-1,0),C(-3,-5),然后根据两点间的距离公式求出AC的长.
解答 解:∵A(0,4),B(-3,0),
∴OA=4,OB=3,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵四边形ABCD为菱形,
∴AD=BC=AB=5,BC∥AD,
∴D(-1,0),C(-3,-5),
∴AC=$\sqrt{(-3-0)^{2}+(-5-4)^{2}}$=3$\sqrt{10}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了坐标与图形性质.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
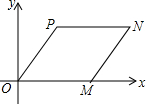 如图所示,在平行直角坐标系中,?OMNP的顶点P坐标是(3,4),顶点M坐标是(4,0)、则顶点N的坐标是( )
如图所示,在平行直角坐标系中,?OMNP的顶点P坐标是(3,4),顶点M坐标是(4,0)、则顶点N的坐标是( )| A. | N(7,4) | B. | N(8,4) | C. | N(7,3) | D. | N(8,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
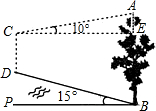 如图,山脚下有一棵树AB,小华从点B沿坡角为15°的坡面上行走50m到达点D,用高为1.5m的测角仪CD测得树顶A的仰角为10°,求树高AB(精确到0.1m)
如图,山脚下有一棵树AB,小华从点B沿坡角为15°的坡面上行走50m到达点D,用高为1.5m的测角仪CD测得树顶A的仰角为10°,求树高AB(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
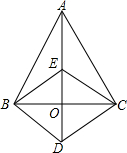 如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE
如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com