
 如图,在△ABC中,∠ACB=90°,AC>BC,M是AB的中点,以CM为直径的⊙O与△ABC的三边分别交于点D、E、F,连接DE、DF,DE与CM交于点P.
如图,在△ABC中,∠ACB=90°,AC>BC,M是AB的中点,以CM为直径的⊙O与△ABC的三边分别交于点D、E、F,连接DE、DF,DE与CM交于点P.分析 (1)利用圆的性质即可直接得出结论;
(2)先设出MP,CP,再用△DOP∽△EMP表示出EP=4$\sqrt{2}$,DE=10$\sqrt{2}$,EM=$\frac{5}{3}$a,再用勾股定理即可建立方程求出a,即可得出结论;
(3)设出AE=m,CM=2r,得出CE=xm,进而得到m=$\frac{4r}{{x}^{2}+1}$,再用△DOP∽△EMP,得出$\frac{OP}{MP}=\frac{DO}{EM}$,从而得出MP=$\frac{m(m-2r)}{m-r}$,CP=2r-MP=$\frac{rm}{m-r}$,即可得出函数关系式.
解答 解:(1)∵∠ACB=90°,
∴DF为⊙O的直径,
∴∠OCF=∠OFC,
∵CM为Rt△ABC斜边上的中线,
∴CM=MB,
∴∠MCB=∠B,
∴∠B=∠OFC,
∴DF∥AB
(2)如图,连接CE,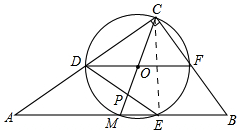
∵$\frac{MP}{CP}$=$\frac{1}{4}$,
∴设MP=a,CP=4a,
∴OP=$\frac{3}{2}$a,OD=$\frac{5}{2}$a,
∵DF∥AB,
∴△DOP∽△EMP,
∴$\frac{OP}{MP}=\frac{DP}{EP}=\frac{DO}{EM}$,
∵DP=6$\sqrt{2}$,
∴EP=4$\sqrt{2}$,
∴DE=10$\sqrt{2}$,EM=$\frac{5}{3}$a,
∵CM为Rt△ABC斜边上的中线,
∴CM=MA,
∴∠A=∠ACM,
∵∠AED=∠ACM,
∴∠A=∠AED,
∴DE=DA,
∵CM为⊙O的直径,
∴CE⊥AB,
∴∠ACE=∠DEC,
∴DE=DC,
∴AC=2DE=20$\sqrt{2}$,
在Rt△ACE和Rt△MCE中,CE2=AC2-AE2,CE2=CM2-ME2,
∴AC2-AE2=CM2-ME2,
∴(20$\sqrt{2}$)2-(5a+$\frac{5}{3}$a)2=(5a)2-($\frac{5}{3}$a)2
∴a=2$\sqrt{3}$,
∴CM=5a=10$\sqrt{3}$;
(3)在Rt△ACE中,tanA=$\frac{CE}{AE}$=x,
设AE=m,CM=2r,
∴CE=xm,
由(2)知,AM=CM=2r,
∴ME=m-2r,
在Rt△MCE中,CE2=CM2-ME2,
∴(xm)2=(2r)2-(m-2r)2,
∴m=$\frac{4r}{{x}^{2}+1}$,
∵△DOP∽△EMP,
∴$\frac{OP}{MP}=\frac{DO}{EM}$,
∴$\frac{r-MP}{MP}=\frac{r}{m-2r}$,
∴MP=$\frac{m(m-2r)}{m-r}$,
∴CP=2r-MP=$\frac{rm}{m-r}$,
∴y=$\frac{MP}{CP}$=-$\frac{1}{2}$x2+$\frac{1}{2}$.
点评 此题是圆的综合题,主要考查了圆中的有关计算,90°的圆周角所对的弦是直径,直角三角形的性质,勾股定理,锐角三角函数,相似三角形的性质和判定,条件较多,难点较大,认真分析条件,准确构造相似三角形是解本题的关键.


科目:初中数学 来源: 题型:解答题
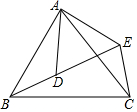 如图,在四边形ABCE中,点D在对角线BE上,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ABD=∠ACE.
如图,在四边形ABCE中,点D在对角线BE上,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ABD=∠ACE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADC的面积为Sl,△ACE的面积为S2,若S△ABC=12,则S1+S2=14.
如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADC的面积为Sl,△ACE的面积为S2,若S△ABC=12,则S1+S2=14.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,将△ABC绕点C逆时针旋转至△A′B′C′,使得点A′恰好落在AB上,A′B′与BC交于点D,则△A′CD的面积为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,将△ABC绕点C逆时针旋转至△A′B′C′,使得点A′恰好落在AB上,A′B′与BC交于点D,则△A′CD的面积为( )| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com