Question

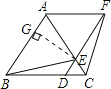
【题目】如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF、BE和CF．
　　　　　　　　　　　　
（1）请在图中找出一对全等三角形，用符号“≌”表示，并加以证明；
（2）判断四边形ABDF是怎样的四边形，并说明理由；
（3）若AB=6，BD=2DC，求四边形ABEF的面积．

Answer 1

【答案】
（1）

【解答】△BDE≌△FEC或△BCE≌△FDC或△ABE≌△ACF

（选证一）△BDE≌△FEC．

证明：∵△ABC是等边三角形，

∴BC=AC，∠ACB=60°．

∵CD=CE，

∴△EDC是等边三角形．

∴DE=EC，∠CDE=∠DEC=60°

∴∠BDE=∠FEC=120°．

又∵EF=AE，

∴BD=FE．

∴△BDE≌△FEC．

（选证二）△BCE≌△FDC．

证明：∵△ABC是等边三角形，

∴BC=AC，∠ACB=60°．

又∵CD=CE，

∴△EDC是等边三角形．

∴∠BCE=∠FDC=60°，DE=CE．

∵EF=AE，

∴EF+DE=AE+CE．

∴FD=AC=BC．

∴△BCE≌△FDC．

（选证三）△ABE≌△ACF．

证明：∵△ABC是等边三角形，

∴AB=AC，∠ACB=∠BAC=60°．

∵CD=CE，∴△EDC是等边三角形．

∴∠AEF=∠CED=60°．

∵EF=AE，△AEF是等边三角形．

∴AE=AF，∠EAF=60°．

∴△ABE≌△ACF．

（2）

【解答】四边形ABDF是平行四边形．

理由：由（1）知，△ABC、△EDC、△AEF都是等边三角形．

∴∠CDE=∠ABC=∠EFA=60°．

∴AB∥DF，BD∥AF．

∴四边形ABDF是平行四边形．

（3）

【解答】由（2）知，四边形ABDF是平行四边形．

∴EF∥AB，EF≠AB．

∴四边形ABEF是梯形．

过E作EG⊥AB于G，则EG=.

∴ S四边形ABEF

．

【解析】（1）从图上及已知条件容易看出△BDE≌△FEC，△BCE≌△FDC，△ABE≌△ACF．判定两个三角形全等时，必须有边的参与，所以此题的关键是找出相等的边．（2）由（1）的结论容易证明AB∥DF，BD∥AF，两组对边分别平行的四边形是平行四边形．（3）EF∥AB，EF≠AB，四边形ABEF是梯形，只要求出此梯形的面积即可．
【考点精析】认真审题，首先需要了解平行四边形的判定(两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形)．