
【题目】张明、王成两位同学在初二学年10次数学单元检测的成绩(成绩均为整数,且个位数为0)如图所示利用图中提供的信息,解答下列问题:
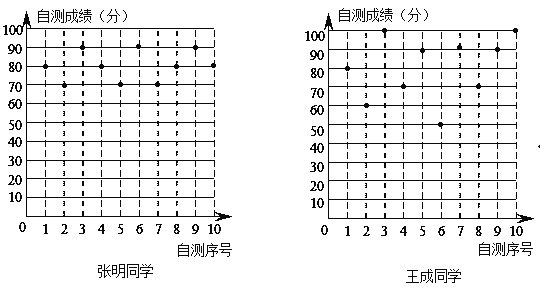
(1)完成下表:
姓名 | 平均成绩 | 中位数 | 众数 | 方差(s2) |
张明 |
| 80 | 80 |
|
王成 |
|
|
| 260 |
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率较高的同学是 ;
(3)根据图表信息,请你对这两位同学各提出学习建议.
【答案】(1)张明:平均成绩80,方,60;王成:平均成绩80,中位,85,众,90;(2)王成;(3)张明学习成绩还需提高,优秀率有待提高.
【解析】
(1)根据平均数、中位数、众数、方差的概念以及求解方法分别求解,填表即可;
(2)分别计算两人的优秀率,然后比较即可;
(3)比较这两位同学的方差,方差越小,成绩越稳定.
(1)张明的平均成绩=(80+70+90+80+70+90+70+80+90+80)÷10=80,
张明的成绩的方差=[4×(80-80)2+3×(70-80)2+3×(90-80)2]÷10=60,
王成的平均成绩=(80+60+100+70+90+50+90+70+90+100)÷10=80,
王成的成绩按大小顺序排列为50、60、70、70、80、90、90、90、100、100,
中间两个数为80,90,则张明的成绩的中位数为85,
王成的成绩中90分出现的次数最多,则王成的成绩的众数为90,
根据相关公式计算出结果,可以填得下表:
姓名 | 平均成绩 | 中位数 | 众数 | 方差(s2) |
张明 | 80 | 80 | 80 | 60 |
王成 | 80 | 85 | 90 | 260 |
(2)如果将90分以上(含90分)的成绩视为优秀,
则张明的优秀率为:3÷10=30%,
王成的优秀率为:5÷10=50%,
所以优秀率较高的同学是王成,
故答案为:王成;
(3)尽管王成同学优秀率较高,但是方差大,说明成绩不稳定,我们可以给他提这样一条参考意见:王成的学习要持之以恒,保持稳定;
相对而言,张明的成绩比较稳定,但是优秀率不及王成,我们可以给他提这样一条参考意见:张明同学的学习还需再加把劲,学习成绩还需提高,优秀率有待提高.


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】如图,C、D是线段AB上两点,已知AC:CD:DB=1:2:3,M、N分别为AC、DB的中点,且AB=12cm,
(1)求线段CD的长;
(2)求线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,AB的垂直平分线MN交AC于点D,若∠A=36°,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ADB是等腰三角形;④△BCD的周长=AB+BC.正确是______(填序号).
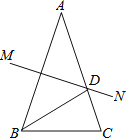
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是( )
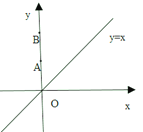
A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:![]() (p,q是正整数,且
(p,q是正整数,且![]() ),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:
),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:![]() .
.
例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=![]() .
.
(1)F(13)= ,F(24)= ;
(2)如果一个两位正整数t,其个位数字是a,十位数字为![]() ,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
(3)在(2)所得“和谐数”中,求F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A,B两点分别在x轴,y轴的正半轴上,且OA=OB,点C在第一象限,OC=3,连接BC,AC,若∠BCA=90°,则BC+AC的值为_________。
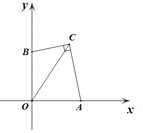
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,分别以AB,AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G在点A,E之间,连接CG,CF,则下列结论不一定正确的是( )

A. △CDF≌△EBC
B. ∠CDF=∠EAF
C. CG⊥AE
D. △ECF是等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com