
如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数 图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
(1)k= ;
(2)试说明AE=BF;
(3)当四边形ABCD的面积为 时,求点P的坐标.
时,求点P的坐标.

(1)3;(2)说明见解析;(3)(1,﹣2).
【解析】
试题分析:(1)根据反比例函数图象上点的坐标特,把B(1,3)代入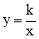 得k=1×3=3.
得k=1×3=3.
(2)设A点坐标为(a,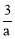 ),易得D点坐标为(0,
),易得D点坐标为(0,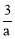 ),P点坐标为(1,
),P点坐标为(1,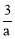 ),C点坐标为(1,0),根据图形与坐标的关系得到PB=3﹣
),C点坐标为(1,0),根据图形与坐标的关系得到PB=3﹣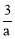 ,PC=﹣
,PC=﹣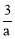 ,PA=1﹣a,PD=1,则可计算出
,PA=1﹣a,PD=1,则可计算出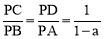 ,加上∠CPD=∠BPA,根据相似的判定得到△PCD∽△PBA,则∠PCD=∠PBA,于是判断CD∥BA,根据平行四边形的判定方法易得四边形BCDE、ADCF都是平行四边形,所以BE=CD,AF=CD,则BE=AF,于是有AE=BF.
,加上∠CPD=∠BPA,根据相似的判定得到△PCD∽△PBA,则∠PCD=∠PBA,于是判断CD∥BA,根据平行四边形的判定方法易得四边形BCDE、ADCF都是平行四边形,所以BE=CD,AF=CD,则BE=AF,于是有AE=BF.
(3)利用四边形ABCD的面积=S△PAB﹣S△PCD得到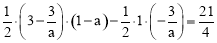 ,整理得2a2+3a=0,然后解方程求出a的值,再写出P点坐标.
,整理得2a2+3a=0,然后解方程求出a的值,再写出P点坐标.
试题解析:【解析】
(1)3.
(2)由(1),反比例函数解析式为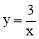 ,
,
∵顶点A在反比例函数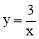 图象上,∴设A点坐标为(
图象上,∴设A点坐标为(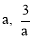 ),
),
∵PB⊥x于点C,PA⊥y于点D,
∴D点坐标为(0,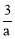 ),P点坐标为(1,
),P点坐标为(1,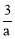 ),C点坐标为(1,0).
),C点坐标为(1,0).
∴PB=3﹣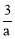 ,PC=﹣
,PC=﹣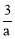 ,PA=1﹣a,PD=1.
,PA=1﹣a,PD=1.
∴ ,∴
,∴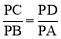 .
.
又∵∠CPD=∠BPA,∴△PCD∽△PBA. ∴∠PCD=∠PBA. ∴CD∥BA.
又∵BC∥DE,AD∥FC,∴四边形BCDE、ADCF都是平行四边形.
∴BE=CD,AF=CD. ∴BE=AF. ∴AF+EF=BE+EF,即AE=BF.
(3)∵四边形ABCD的面积=S△PAB﹣S△PCD,
∴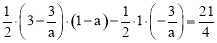 .
.
整理得2a2+3a=0,解得a1=0(舍去),a2=﹣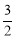 .
.
∴P点坐标为(1,﹣2).
考点:1.反比例函数综合题;2.曲线上点的坐标与方程的关系;3.相似三角形的判定和性质;4.平行四边形的判定和性质;5.转换思想和方程思想的应用.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源:2014年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:解答题
如图,二次函数y=ax2+bx(a<0)的图象过坐标原点O,与x轴的负半轴交于点A,过A点的直线与y轴交于B,与二次函数的图象交于另一点C,且C点的横坐标为﹣1,AC:BC=3:1.
(1)求点A的坐标;
(2)设二次函数图象的顶点为F,其对称轴与直线AB及x轴分别交于点D和点E,若△FCD与△AED相似,求此二次函数的关系式.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:选择题
已知A样本的数据如下:72,73,76,76,77,78,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
A.平均数 B.标准差 C.中位数 D.众数
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏徐州卷)数学(解析版) 题型:解答题
甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
| 平均数 | 众数 | 中位数 | 方差 |
甲 | 8 |
| 8 | 0.4 |
乙 |
| 9 |
| 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏徐州卷)数学(解析版) 题型:填空题
在平面直角坐标系中,将点A(4,2)绕原点逆时针方向旋转90°后,其对应点A′的坐标为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:解答题
我们用 表示不大于
表示不大于 的最大整数,例如:
的最大整数,例如: ,
, ,
, ;用
;用 表示大于
表示大于 的最小整数,例如:
的最小整数,例如: ,
, ,
,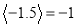 .解决下列问题:
.解决下列问题:
(1) = ,,
= ,, = ;
= ;
(2)若 =2,则
=2,则 的取值范围是 ;若
的取值范围是 ;若 =-1,则
=-1,则 的取值范围是 ;
的取值范围是 ;
(3)已知 ,
, 满足方程组
满足方程组 ,求
,求 ,
, 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:填空题
某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是 分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com