
【题目】如图,抛物线y=a( x+1 )2-4a(a<0)与x轴交于点A、B(A在B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,连接BD交抛物线的对称轴于点E,连接BC、CE.
(1)抛物线顶点坐标为 (用含a的代数式表示),A点坐标为 ,
(2)当△DCE的面积为![]() 时,求a的值;
时,求a的值;
(3)当△BCE为直角三角形时,求抛物线的解析式.

【答案】(1)(-1,-4a),(-3,0)(2)-![]() (3)y=-( x+1 )2+4或y=-
(3)y=-( x+1 )2+4或y=-![]() ( x+1 )2 +
( x+1 )2 +![]()
【解析】分析:(1)由抛物线的性质,直接得到顶点坐标.令y=0,即可求得A点坐标.
(2)设对称轴交CD于M,交x轴于F,得到C(0,-3a).由对称轴为直线x=1,得到D(-2,-3a),由△DCE的面积=![]() ,得到ME的长,即可得到E的坐标,易求直线BD的解析式为:
,得到ME的长,即可得到E的坐标,易求直线BD的解析式为:![]() .由E为直线BD与对称轴的交点,即可得到a的值.
.由E为直线BD与对称轴的交点,即可得到a的值.
(3)作DH⊥x轴于H.显然,∠CBE为锐角,所以∠CBE![]() 90°.分两种情况讨论:
90°.分两种情况讨论:
①若∠BEC=90°,②若∠BCE=90°。
详解:(1)抛物线y=a( x+1 )2-4a(a<0)的顶点坐标是(-1,-4a).令y=0,得:a( x+1 )2-4a=0,解得:x=-3,或x=1,∴A点坐标为(-3,0).
(2)设对称轴交CD于M,交x轴于F.令x=0,得:y=a-4a=-3a,∴C(0,-3a).∵对称轴为直线x=1,∴D(-2,-3a),∴DC=2.∵△DCE的面积=![]() ,∴
,∴![]() DCME=
DCME=![]() ,∴ME=
,∴ME=![]() ,∴E(-1,
,∴E(-1,![]() ),易求直线BD的解析式为:
),易求直线BD的解析式为:![]() .∵E为直线BD与对称轴的交点,∴当x=-1时,y=-2a,∴-2a=
.∵E为直线BD与对称轴的交点,∴当x=-1时,y=-2a,∴-2a=![]() ,解得:a=
,解得:a=![]() .
.
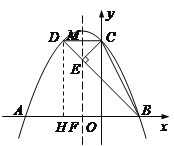
(3)作DH⊥x轴于H.
显然,∠CBE为锐角,所以∠CBE![]() 90°.
90°.
①若∠BEC=90°,则∠DEC=90°.
∵CD∥x轴,∴由对称性可知∠CEM=∠DEM=45°,∴∠BEF=45°,∴∠BDH=45°,∴BH=DH.
∵y=a( x+1 )2-4a,∴A(-3,0),B(1,0),C(0,-3a),抛物线的对称轴为直线x=-1,∴D(-2,-3a),∴BH=3,DH=-3a,∴a=-1∴y=-( x+1 )2+4;
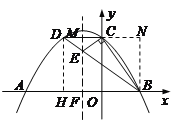
②若∠BCE=90°,作BN⊥DC交DC的延长线于N,则∠BCN+∠ECM=∠BCN+∠EDM=∠BDH+∠EDM=90°,∴∠BCN=∠BDH,∴Rt△BCN∽Rt△BDH,∴BN:CN=BH:DH ,∴-3a:1=3:-3a,∴a=![]() ,∴ y=
,∴ y=![]() ( x+1 )2 .
( x+1 )2 .
综上所述:y=-( x+1 )2+4或![]() .
.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】![]() 村有肥料200吨,
村有肥料200吨,![]() 村有肥料300吨,现要将这些肥料全部运往
村有肥料300吨,现要将这些肥料全部运往![]() 、
、![]() 两仓库.从
两仓库.从![]() 村往
村往![]() 、
、![]() 两仓库运肥料的费用分别为每吨20元和25元;从
两仓库运肥料的费用分别为每吨20元和25元;从![]() 村往
村往![]() 、
、![]() 两仓库运肥料的费用分别为每吨15元和18元;现
两仓库运肥料的费用分别为每吨15元和18元;现![]() 仓库需要肥料240吨,现
仓库需要肥料240吨,现![]() 仓库需要肥料260吨.
仓库需要肥料260吨.
(1)设![]() 村运往
村运往![]() 仓库
仓库![]() 吨肥料,
吨肥料,![]() 村运肥料需要的费用为
村运肥料需要的费用为![]() 元;
元;![]() 村运肥料需要的费用为
村运肥料需要的费用为![]() 元.
元.
①写出![]() 、
、![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
②试讨论![]() 、
、![]() 两村中,哪个村的运费较少?
两村中,哪个村的运费较少?
(2)考虑到![]() 村的经济承受能力,
村的经济承受能力,![]() 村的运输费用不得超过4830元,设两村的总运费为
村的运输费用不得超过4830元,设两村的总运费为![]() 元,怎样调运可使总运费最少?
元,怎样调运可使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
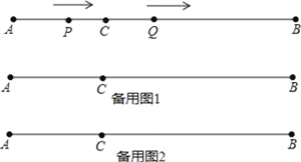
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角尺的直角顶点O叠放在一起。
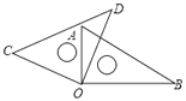
(1)若∠AOD=25°,则∠AOC= 65° ,∠BOD= ,∠BOC= ;
(2)比较∠AOC与∠BOD的大小关系,并说明理由;
(3)猜想∠AOD与∠BOC的数量关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,过B点作射线BE,过C点作射线CF,使∠ABE=∠ACF,且射线BE,CF交于点D,过A点作AM⊥BD于M.
⑴如图1所示,若BE⊥CF,AB=6,∠ABE=30°,求CD;
⑵如图2所示,求证:BM=DM﹣DC.
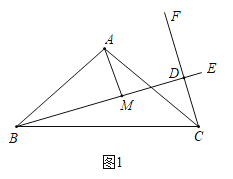
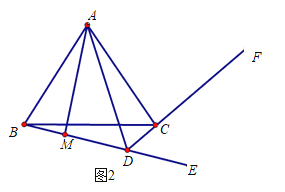
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽暑假期间参加社会实践活动,从某批发市场以批发价每个m元的价格购进100个手机充电宝,然后每个加价n元到市场出售(结果用含m,n的式子表示)
(1)求售出100个手机充电宝的总售价为多少元?
(2)由于开学临近,小丽在成功售出60个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.(注:售价的8折即按原售价的80%出售)
①她的总销售额是多少元?
②假如不采取降价销售,且也全部售完,她将比实际销售多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,![]()
![]() ……,都是斜边在
……,都是斜边在![]() 轴上,斜边长分别为2,4,6……的等腰直角三角形,若
轴上,斜边长分别为2,4,6……的等腰直角三角形,若![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,则依图中所示规律,
,则依图中所示规律,![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC,BD相交于O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论

①BE⊥AC
②四边形BEFG是平行四边形
③EG=GF
④EA平分∠GEF
其中正确的是( )
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”.
(提出问题)三个有理数a、b、c满足abc>0,求![]() 的值.
的值.
(解决问题)由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即a>0,b>0,c>0时,
则:![]() =
=![]() =1+1+1=3;
=1+1+1=3;
②当a,b,c有一个为正数,另两个为负数时,设a>0,b<0,c<0,
即:![]() =
=![]() =1+(1)+(1)=1,所以
=1+(1)+(1)=1,所以![]() 的值为3或1.
的值为3或1.
(探究)请根据上面的解题思路解答下面的问题:
(1)已知a<0,b>0,c>0,则![]() ,
,![]() ,
,![]() ;
;
(2)三个有理数a,b,c满足abc<0,求![]() 的值;
的值;
(3)已知|a|=3,|b|=1,且a<b,求a+b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com