练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】小丽暑假期间参加社会实践活动，从某批发市场以批发价每个m元的价格购进100个手机充电宝，然后每个加价n元到市场出售(结果用含m，n的式子表示)

    (1)求售出100个手机充电宝的总售价为多少元?

    (2)由于开学临近，小丽在成功售出60个充电宝后，决定将剩余充电宝按售价8折出售，并很快全部售完.(注:售价的8折即按原售价的80%出售)

    ①她的总销售额是多少元?

    ②假如不采取降价销售，且也全部售完，她将比实际销售多盈利多少元?

    【答案】(1) 100(m+n)元;(2) ①92(m+n)(元); ②8(m+n)(元)

    【解析】

    （1）根据总售价=销售单价×数量列出代数式即可；

    （2）①根据（1）的方式分别列出前60个和剩余的40个充电宝的销售额，再把两式子相加，最后整理即可；②列出不降价销售的式子减去①中降价的总销售额即可得出答案.

    （1）每个手机充电宝的售价为元，则售出个手机充电宝的总售价为 元；

    （2）①她的总销售额是： (元)

    ②她将比实际销售多盈利： (元)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】股民王晓宇上周五在股市以收盘价（股市收市时的价格）每股24元购买进某公司股票1000股，周六、周日股市不交易，在接下来的一周交易日内，王晓宇记下该股每日收盘价格相比前一天的涨跌情况如下表：（单位：元）

    （1）星期三收盘时，每股是多少元？

    （2）已知小明父亲买进股票时付了1.5‰的手续费，卖出时需付成交额的1.5‰的手续费和1‰的交易税，如果他在周五收盘前将全部股票卖出，他的收益情况如何？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，数轴上的点A，O，B，C，D分别表示－3，0,2.5,5，－6.

    (1)求B，O两点间的距离；

    (2)求A，D两点间的距离；

    (3)求C，B两点间的距离；

    (4)请观察思考，若点A表示数m，且m<0，点B表示数n，且n>0，用含m，n的代数式表示A，B两点间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】莲城超市以10元/件的价格调进一批商品，根据前期销售情况，每天销售量y（件）与该商品定价x（元）是一次函数关系，如图所示．

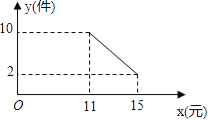
    （1）求销售量y与定价x之间的函数关系式；

    （2）如果超市将该商品的销售价定为13元/件，不考虑其它因素，求超市每天销售这种商品所获得的利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数y=x的图象上，从左向右第3个正方形中的一个顶点A的坐标为（8，4），阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn，则Sn的值为__．（用含n的代数式表示，n为正整数）

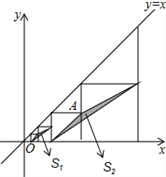
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l1的函数解析式为y=﹣2x+4，且l1与x轴交于点D，直线l2经过点A、B，直线l1、l2交于点C．

    （1）求直线l2的函数解析式；

    （2）求△ADC的面积；

    （3）在直线l2上是否存在点P，使得△ADP面积是△ADC面积的2倍？如果存在，请求出P坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个大正方形和四个全等的小正方形按图①、②两种方式摆放，设小正方形的边长为x，请仔细观察图形回答下列问题．
    （1）用含a、b的代数式表示x，则x=____．
    （2）用含a、b的代数式表示大正方形的边长____．（请将结果化为最简）
    （3）利用前两问的结论求出图②的大正方形中未被小正方形覆盖部分的面积．（用a、b的代数式表示）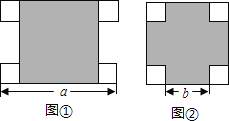

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题提出

    （1）如图1，点A为线段BC外一动点，且BC=a，AB=b，填空：当点A位于　 　时，线段AC的长取得最大值，且最大值为　 　（用含a，b的式子表示）．

    问题探究

    （2）点A为线段BC外一动点，且BC=6，AB=3，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE，找出图中与BE相等的线段，请说明理由，并直接写出线段BE长的最大值．

    问题解决：

    （3）①如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，求线段AM长的最大值及此时点P的坐标．

    ②如图4，在四边形ABCD中，AB=AD，∠BAD=60°，BC=4，若对角线BD⊥CD于点D，请直接写出对角线AC的最大值．

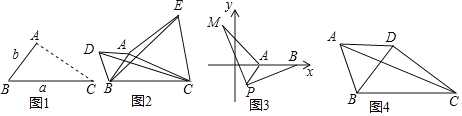
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1，图2，图3是三张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，两点都在格点上，连结，请完成下列作图：

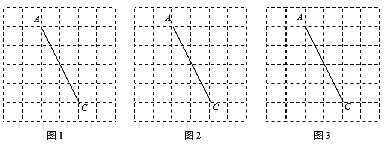
    (1)以为对角线在图1中作一个正方形，且正方形各顶点均在格点上.

    (2)以为对角线在图2中作一个矩形，使得矩形面积为6，且矩形各顶点均在格点上.

    (3)以为对角线在图3中作一个面积最小的平行四边形，且平行四边形各顶点均在格点上.

    查看答案和解析>>

    同步练习册答案