
【题目】问题提出
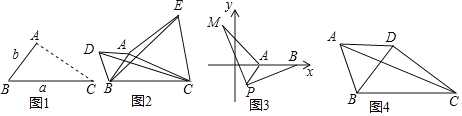
(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示).
问题探究
(2)点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
问题解决:
(3)①如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
②如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
【答案】(1)CB的延长线上,a+b;(2)①CD=BE,②9;(3)P(2﹣![]() ,
,![]() )(4)AC的最大值为2
)(4)AC的最大值为2![]() +2
+2![]()
【解析】试题分析:(1)根据点A位于CB的延长线上时,线段AC的长取得最大值,即可得到结论;
(2)①根据等边三角形的性质得到AD=AB,AC=AE,∠BAD=∠CAE=60°,推出△CAD≌△EAB,根据全等三角形的性质得到CD=BE;②由于线段BE长的最大值=线段CD的最大值,根据(1)中的结论即可得到结果;
(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,得到△APN是等腰直角三角形,根据全等三角形的性质得到PN=PA=2,BN=AM,根据当N在线段BA的延长线时,线段BN取得最大值,即可得到最大值为2![]() +3;过P作PE⊥x轴于E,根据等腰直角三角形的性质,即可得到结论;
+3;过P作PE⊥x轴于E,根据等腰直角三角形的性质,即可得到结论;
(4)如图4中,以BC为边作等边三角形△BCM,由△ABC≌△DBM,推出AC=MD,推出欲求AC的最大值,只要求出DM的最大值即可,由BC=4![]() =定值,∠BDC=90°,推出点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大;
=定值,∠BDC=90°,推出点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大;
试题解析:解:(1)∵点A为线段BC外一动点,且BC=a,AB=b,∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b.故答案为:CB的延长线上,a+b;
(2)①CD=BE,理由:∵△ABD与△ACE是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.在△CAD与△EAB中,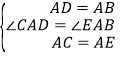 ,∴△CAD≌△EAB(SAS),∴CD=BE;
,∴△CAD≌△EAB(SAS),∴CD=BE;
②∵线段BE长的最大值=线段CD的最大值,∴由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,∴最大值为BD+BC=AB+BC=3+6=9;
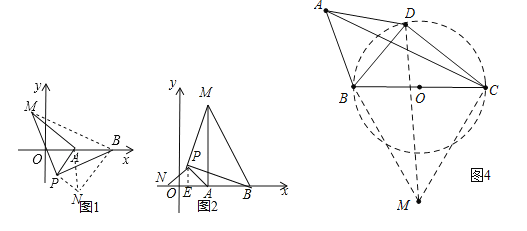
(3)如图1,连接BM.∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,则△APN是等腰直角三角形,∴PN=PA=2,BN=AM.∵A的坐标为(2,0),点B的坐标为(5,0),∴OA=2,OB=5,∴AB=3,∴线段AM长的最大值=线段BN长的最大值,∴当N在线段BA的延长线时,线段BN取得最大值,最大值=AB+AN.∵AN=![]() AP=2
AP=2![]() ,∴最大值为2
,∴最大值为2![]() +3;
+3;
如图2,过P作PE⊥x轴于E.∵△APN是等腰直角三角形,∴PE=AE=![]() ,∴OE=BO﹣AB﹣AE=5﹣3﹣
,∴OE=BO﹣AB﹣AE=5﹣3﹣![]() =2﹣
=2﹣![]() ,∴P(2﹣
,∴P(2﹣![]() ).
).
(4)如图4中,以BC为边作等边三角形△BCM.∵∠ABD=∠CBM=60°,∴∠ABC=∠DBM.∵AB=DB,BC=BM,∴△ABC≌△DBM,∴AC=MD,∴欲求AC的最大值,只要求出DM的最大值即可.∵BC=4![]() =定值,∠BDC=90°,∴点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2
=定值,∠BDC=90°,∴点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2![]() +2
+2![]() ,∴AC的最大值为2
,∴AC的最大值为2![]() +2
+2![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
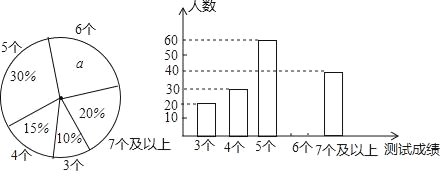
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a= %,并补全条形图;
(2)在这次抽测中,测试成绩的众数和中位数分别是 个、 个.
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽暑假期间参加社会实践活动,从某批发市场以批发价每个m元的价格购进100个手机充电宝,然后每个加价n元到市场出售(结果用含m,n的式子表示)
(1)求售出100个手机充电宝的总售价为多少元?
(2)由于开学临近,小丽在成功售出60个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.(注:售价的8折即按原售价的80%出售)
①她的总销售额是多少元?
②假如不采取降价销售,且也全部售完,她将比实际销售多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的斜边BC为边,在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.若AB=4,AO=6![]() ,则AC的长等于( )
,则AC的长等于( )
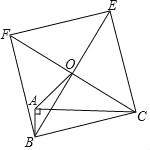
A. 12![]() B. 16C. 8+6
B. 16C. 8+6![]() D. 4+6
D. 4+6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输部门规定:办理托运,当一件物品的重量不超过![]() 千克时,需付基础费
千克时,需付基础费![]() 元和保险费
元和保险费![]() 元;为了限制过重物品的托运,当一件物品的重量超过
元;为了限制过重物品的托运,当一件物品的重量超过![]() 千克时,除了付以上基础费和保险费外,超过部分每千克还需付
千克时,除了付以上基础费和保险费外,超过部分每千克还需付![]() 元的超重费.设某件物品的重量为
元的超重费.设某件物品的重量为![]() 千克,支付费用为
千克,支付费用为![]() 元.
元.
(1)当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
(2)甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:
托运人 | 物品重量/千克 | 支付费用/元 |
甲 | 14 | 33 |
乙 | 20 | 39 |
丙 | 30 |
|
根据以上提供的信息确定![]() 的值,并计算出丙所支付的费用
的值,并计算出丙所支付的费用![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”期间,小明一家自驾游去了离家200km的某地,如图是他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象.根据图象,解答下列问题:
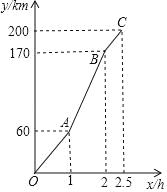
(1)点A的实际意义是 ;
(2)求出线段AB的函数表达式;
(3)他们出发2.3h时,距目的地还有多少km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
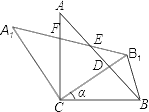
【题目】如图,△ABC中,∠ACB=90,AC=BC,将△ABC绕点C逆时针旋转α角(0<α<90)得到△A1B1C,连结BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F,
(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以证明(△ABC与△A1B1C全等除外);
(2)当△BB1D是等腰三角形时,求α.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com