
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
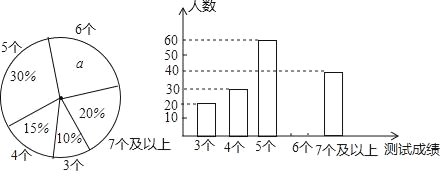
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a= %,并补全条形图;
(2)在这次抽测中,测试成绩的众数和中位数分别是 个、 个.
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
【答案】(1)25,补图详见解析;(2)5,5;(3)810.
【解析】
(1)根据扇形统计图可以求得a的值,根据扇形统计图和条形统计图可以得到做6个的学生数,从而可以将条形图;
(2)根据(1)中补全的条形图可以得到众数和中位数;
(3)根据统计图可以估计该区体育中考中选报引体向上的男生能获得满分的人数.
解:(1)扇形统计图中a=1﹣30%﹣15%﹣10%﹣20%=25%,
设引体向上6个的学生有x人,由题意得
![]() ,解得x=50.
,解得x=50.
条形统计图补充如下:

(2)由条形图可知,引体向上5个的学生有60人,人数最多,所以众数是5;
共200名同学,排序后第100名与第101名同学的成绩都是5个,故中位数为(5+5)÷2=5
(3)![]() ×1800=810(名).
×1800=810(名).
答:估计该区体育中考选报引体向上的男生能获得满分的同学有810名.
故答案为:25;5,5.


科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民王晓宇上周五在股市以收盘价(股市收市时的价格)每股24元购买进某公司股票1000股,周六、周日股市不交易,在接下来的一周交易日内,王晓宇记下该股每日收盘价格相比前一天的涨跌情况如下表:(单位:元)

(1)星期三收盘时,每股是多少元?
(2)已知小明父亲买进股票时付了1.5‰的手续费,卖出时需付成交额的1.5‰的手续费和1‰的交易税,如果他在周五收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数 y1=kx+b 与 y2=x+a 的图象如图所示,则下列结论:①k<0;②a<0,b<0;③当 x=3 时,y1=y2;④不等式 kx+b>x+a 的解集是 x<3,其中正确的结论有_______.(只填序号)
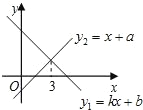
查看答案和解析>>
科目:初中数学 来源: 题型:
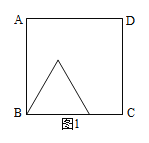
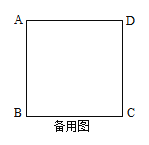
【题目】如图1,图2中,正方形ABCD的边长为6,点P从点B出发沿边BC—CD以每秒2个单位长的速度向点D匀速运动,以BP为边作等边三角形BPQ,使点Q在正方形ABCD内或边上,当点Q恰好运动到AD边上时,点P停止运动。设运动时间为t秒(t≥0)。
(1)当t=2时,点Q到BC的距离=_____;
(2)当点P在BC边上运动时,求CQ的最小值及此时t的值;
(3)若点Q在AD边上时,如图2,求出t的值;
(4)直接写出点Q运动路线的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A,O,B,C,D分别表示-3,0,2.5,5,-6.
![]()
(1)求B,O两点间的距离;
(2)求A,D两点间的距离;
(3)求C,B两点间的距离;
(4)请观察思考,若点A表示数m,且m<0,点B表示数n,且n>0,用含m,n的代数式表示A,B两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】莲城超市以10元/件的价格调进一批商品,根据前期销售情况,每天销售量y(件)与该商品定价x(元)是一次函数关系,如图所示.
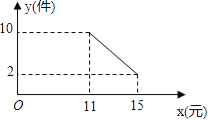
(1)求销售量y与定价x之间的函数关系式;
(2)如果超市将该商品的销售价定为13元/件,不考虑其它因素,求超市每天销售这种商品所获得的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
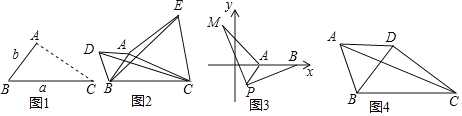
(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示).
问题探究
(2)点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
问题解决:
(3)①如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
②如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com