
����Ŀ��ij���䲿�Ź涨���������ˣ���һ����Ʒ������������![]() ǧ��ʱ���踶������
ǧ��ʱ���踶������![]() Ԫ�ͱ��շ�
Ԫ�ͱ��շ�![]() Ԫ��Ϊ�����ƹ�����Ʒ�����ˣ���һ����Ʒ����������
Ԫ��Ϊ�����ƹ�����Ʒ�����ˣ���һ����Ʒ����������![]() ǧ��ʱ�����˸����ϻ����Ѻͱ��շ��⣬��������ÿǧ�˻��踶
ǧ��ʱ�����˸����ϻ����Ѻͱ��շ��⣬��������ÿǧ�˻��踶![]() Ԫ�ij��ط�.��ij����Ʒ������Ϊ
Ԫ�ij��ط�.��ij����Ʒ������Ϊ![]() ǧ�ˣ�֧������Ϊ
ǧ�ˣ�֧������Ϊ![]() Ԫ.
Ԫ.
��1����![]() ʱ��
ʱ��![]() ______________����ʽ�ӱ�ʾ����
______________����ʽ�ӱ�ʾ����
��![]() ʱ��
ʱ��![]() ______________����ʽ�ӱ�ʾ����
______________����ʽ�ӱ�ʾ����
��2���ס��ҡ������˸�����һ����Ʒ����Ʒ��������֧���������±���ʾ��
������ | ��Ʒ����/ǧ�� | ֧������/Ԫ |
�� | 14 | 33 |
�� | 20 | 39 |
�� | 30 |
|
���������ṩ����Ϣȷ��![]() ��ֵ�������������֧���ķ���
��ֵ�������������֧���ķ���![]() .
.
���𰸡���1��b��30��b��30����x18��c����2��b=3,c=3,w=69Ԫ
��������
��1����x��18ʱ��ֻ�踶������30Ԫ�����շ�bԪ������֧������Ϊ��b��30��Ԫ����x��18ʱ���踶����Ϊ������30Ԫ�����շ�bԪ�����طѣ���[b��30����x18��c]Ԫ��
��2�����ݱ���������г���Ԫһ�η��������b,c�������.
�⣺��1����![]() ʱ��
ʱ��![]() b��30
b��30
��![]() ʱ��
ʱ��![]() b��30����x18��c��
b��30����x18��c��
���b��30��b��30����x18��c��
��2���������
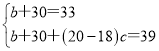 ��
��
��ã�![]() ��
��
����֧���ķ���![]() = 3��30��3��3018��=69��Ԫ��
= 3��30��3��3018��=69��Ԫ��
��b=3,c=3,w=69Ԫ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
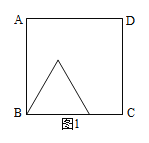
����Ŀ����ͼ1��ͼ2�У�������ABCD�ı߳�Ϊ6����P�ӵ�B�����ر�BC��CD��ÿ��2����λ�����ٶ����D�����˶�����BPΪ�����ȱ�������BPQ��ʹ��Q��������ABCD�ڻ���ϣ�����Qǡ���˶���AD����ʱ����Pֹͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����t��2ʱ����Q��BC�ľ��룽_____��
��2������P��BC�����˶�ʱ����CQ����Сֵ����ʱt��ֵ��
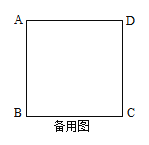
��3������Q��AD����ʱ����ͼ2�����t��ֵ��
��4��ֱ��д����Q�˶�·�ߵij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
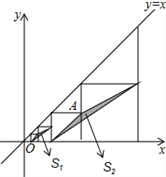
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߳����ȵ��������������У�ÿ�������ζ���һ���������ں���y=x��ͼ���ϣ��������ҵ�3���������е�һ������A������Ϊ��8��4������Ӱ�����β��ֵ���������������μ�ΪS1��S2��S3������Sn����Sn��ֵΪ__�����ú�n�Ĵ���ʽ��ʾ��nΪ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���������κ��ĸ�ȫ�ȵ�С�����ΰ�ͼ�١������ַ�ʽ�ڷţ���С�����εı߳�Ϊx������ϸ�۲�ͼ�λش��������⣮
��1���ú�a��b�Ĵ���ʽ��ʾx����x=____��
��2���ú�a��b�Ĵ���ʽ��ʾ�������εı߳�____�����뽫�����Ϊ���
��3������ǰ���ʵĽ������ͼ�ڵĴ���������δ��С�����θ��Dz��ֵ����������a��b�Ĵ���ʽ��ʾ��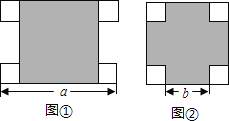
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������е��ش���̩������ⷿ������½���������ƻ�10���ڽ����������Ⱥ��ס�����⣬ǰ6�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=![]() x+5����x��λ���꣬1��x��6��xΪ����������4�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=-
x+5����x��λ���꣬1��x��6��xΪ����������4�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=-![]() x+
x+![]() ��x��λ���꣬7��x��10��xΪ������������ÿ��Ĺ��ⷿȫ�������꣮���⣬����������ǵ����ص�Ӱ�죬ÿ������Ҳ��֮�ϵ���Ԥ�ƣ���x��Ͷ��ʹ�õĹ��ⷿ�����z����λ��Ԫ/m2����ʱ��x����λ���꣬1��x��10��xΪ����������һ�κ�����ϵ���±���
��x��λ���꣬7��x��10��xΪ������������ÿ��Ĺ��ⷿȫ�������꣮���⣬����������ǵ����ص�Ӱ�죬ÿ������Ҳ��֮�ϵ���Ԥ�ƣ���x��Ͷ��ʹ�õĹ��ⷿ�����z����λ��Ԫ/m2����ʱ��x����λ���꣬1��x��10��xΪ����������һ�κ�����ϵ���±���
z��Ԫ/m2�� | 50 | 52 | 54 | 56 | 58 | �� |
x���꣩ | 1 | 2 | 3 | 4 | 5 | �� |
��1�����z��x�ĺ�����ϵʽ��
��2���������ڵڼ���Ͷ��Ĺ��ⷿ��ȡ�������࣬���Ϊ���ٰ���Ԫ��
��3������6�꿢��Ͷ��ʹ�õĹ��ⷿ�ɽ��20���˵�ס�����⣬�����ƻ��ڵ�10��Ͷ��Ĺ��ⷿ��������������£�Ҫ���˾�ס������ȵ�6���˾�ס��������a%�������ɽ��ס�����������ȵ�6�����1.35a%����a��ֵ��
���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������
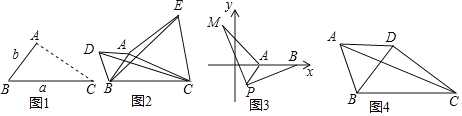
��1����ͼ1����AΪ�߶�BC��һ���㣬��BC=a��AB=b����գ�����Aλ���� ��ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪ�� �����ú�a��b��ʽ�ӱ�ʾ����
����̽��
��2����AΪ�߶�BC��һ���㣬��BC=6��AB=3����ͼ2��ʾ���ֱ���AB��ACΪ�ߣ����ȱ�������ABD�͵ȱ�������ACE������CD��BE���ҳ�ͼ����BE��ȵ��߶Σ���˵�����ɣ���ֱ��д���߶�BE�������ֵ��
��������
��3������ͼ3����ƽ��ֱ������ϵ�У���A������Ϊ��2��0������B������Ϊ��5��0������PΪ�߶�AB��һ���㣬��PA=2��PM=PB����BPM=90�㣬���߶�AM�������ֵ����ʱ��P�����꣮
����ͼ4�����ı���ABCD�У�AB=AD����BAD=60�㣬BC=4![]() �����Խ���BD��CD�ڵ�D����ֱ��д���Խ���AC�����ֵ��
�����Խ���BD��CD�ڵ�D����ֱ��д���Խ���AC�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵxOy�У����ڵ�P��x��y����Q����x��y�������������¶��壺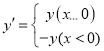 ���Ƶ�QΪ��P�����ɿر���������磺�㣨1��2�������ɿر����Ϊ�㣨��1��2�����㣨��1��2�������ɿر����Ϊ�㣨1����2��
���Ƶ�QΪ��P�����ɿر���������磺�㣨1��2�������ɿر����Ϊ�㣨��1��2�����㣨��1��2�������ɿر����Ϊ�㣨1����2��
���ݶ��壬����������⣻
��1���㣨3��4�������ɿر����Ϊ���� ����
��2����P1�����ɿر����Ϊ��P2����P2�����ɿر����Ϊ��P3����P3�����ɿر����Ϊ��P4�������Դ����ƣ�����P2018������Ϊ��3��a�������P1������Ϊ�� ����
��3������N��a��3���Ǻ���y����x+4ͼ���ϵ�M�����ɿر���������M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��ͼ��1����һ����Ϊ2m����Ϊ2n�ľ��Σ��Ѵ˾�����ͼ�������ü�������Ϊ�ĸ�С�����Σ�Ȼ��ͼ��2������״ƴ��һ���������Σ����ʣ�������ͼ�ε�ʲô�����䣿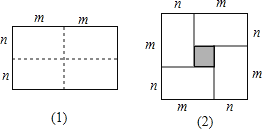
��2�������õĴ������������ԭ���ε�����������Ӱ���ֵ�����ú�m��n�Ĵ���ʽ��ʾΪ��m-n��2��m2-2mn+n2 ��
��3����ǰ���̽���ɵó��Ľ����ǣ����ܳ�һ���ľ����У��� ʱ��������
��4�������ε��ܳ�Ϊ24cm���߳�Ϊ����ʱ����ͼ�ε��������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
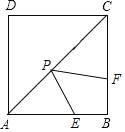
����Ŀ����ͼ��������ABCD�У�AB��8����E��F�ֱ��ڱ�AB��BC�ϣ�BE��BF��2����P�ǶԽ���AC�ϵ�һ�����㣬��PE+PF����Сֵ��_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com