
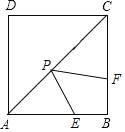
【题目】如图,正方形ABCD中,AB=8,点E、F分别在边AB、BC上,BE=BF=2,点P是对角线AC上的一个动点,则PE+PF的最小值是_____.
【答案】4![]()
【解析】
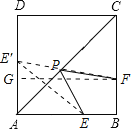
过E作AC的垂线交AD于点E′,连接E′F交AC于点P,过F作AD的垂线交AD于点G,则E′F即为所求,根据正方形的性质可知△AEE′是等腰三角形,AE′=6,GA=BF=2,即可求出GE′的长,再由勾股定理即可求出E′F的长.
解:过E作AC的垂线交AD于点E′,连接E′F交AC于点P,过F作AD的垂线交AD于点G,则E′F即为所求,
∵四边形ABCD是正方形,
∴∠DAC=∠BAC=45°,
∵EE′⊥AC,
∴△AEE′是等腰三角形,
∴AE=AE′=8﹣2=6,
∵GF⊥AD,
∴GA=BF=2,
∴GE′=AE'﹣AG=6﹣2=4,
在Rt△GFE′中,GE′=4,GF=8,
∴E′F=![]() .
.
故答案为:![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】某运输部门规定:办理托运,当一件物品的重量不超过![]() 千克时,需付基础费
千克时,需付基础费![]() 元和保险费
元和保险费![]() 元;为了限制过重物品的托运,当一件物品的重量超过
元;为了限制过重物品的托运,当一件物品的重量超过![]() 千克时,除了付以上基础费和保险费外,超过部分每千克还需付
千克时,除了付以上基础费和保险费外,超过部分每千克还需付![]() 元的超重费.设某件物品的重量为
元的超重费.设某件物品的重量为![]() 千克,支付费用为
千克,支付费用为![]() 元.
元.
(1)当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
(2)甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:
托运人 | 物品重量/千克 | 支付费用/元 |
甲 | 14 | 33 |
乙 | 20 | 39 |
丙 | 30 |
|
根据以上提供的信息确定![]() 的值,并计算出丙所支付的费用
的值,并计算出丙所支付的费用![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
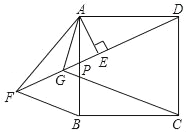
【题目】如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
(1)求证:△AEG是等腰直角三角形;
(2)求证:AG+CG=![]() DG.
DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工厂今年一月份产量相同,都是a吨,三月份的产量也相同,甲厂每月产量增长的百分数(和上月相比)相同,乙厂每月产量增长的吨数(和上月相比)相同
(1)如果上述百分数是20%,那么甲厂三月份产量是多少?(结果可以含有a)
(2)如果上述百分数是-20%,那么乙厂二月份产量是多少?(结果可以含有a)
查看答案和解析>>
科目:初中数学 来源: 题型:
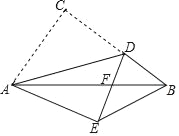
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线AB:y![]() x+4交x轴于点A,交y轴于点B.直线CD:y
x+4交x轴于点A,交y轴于点B.直线CD:y![]() x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.
(1)直接写出点B和点D的坐标;
(2)若点P是射线MD上的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系;
(3)当S=20时,平面直角坐标系内是否存在点E,使以点B、E、P、M为顶点的四边形是平行四边形?若存在,请直接写出所有符合条件的点E的坐标;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com