
【题目】平面直角坐标系xOy中,对于点P(x,y)和Q(﹣x,y′),给出如下定义: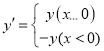 ,称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(﹣1,2),点(﹣1,2)的“可控变点”为点(1,﹣2)
,称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(﹣1,2),点(﹣1,2)的“可控变点”为点(1,﹣2)
根据定义,解答下列问题;
(1)点(3,4)的“可控变点”为点 .
(2)点P1的“可控变点”为点P2,点P2的“可控变点”为点P3,点P3的“可控变点”为点P4,…,以此类推.若点P2018的坐标为(3,a),则点P1的坐标为 .
(3)若点N(a,3)是函数y=﹣x+4图象上点M的“可控变点”,求点M的坐标.
【答案】(1)(-3,4),(2)(-3,a),(3)(1,3).
【解析】
(1)依据“可控变点”的定义可得,点(3,4)的“可控变点”为点(﹣3,4);
(2)依据变化规律可得每四次变化出现一次循环,即可得到当点P2018的坐标为(3,a),则点P1的坐标为(﹣3,﹣a);
(3)分两种情况讨论:当﹣a≥0时,a≤0;当﹣a<0时,a>0,分别把点M的坐标代入函数y=﹣x+4即可得到结论.
解:(1)∵x=3>0,
∴根据“可控变点”的定义可得,点(3,4)的“可控变点”为点(﹣3,4),
故答案为:(﹣3,4);
(2)当x≥0时,点P1(x,y)的“可控变点”为点P2(﹣x,y),点P2(﹣x,y)的“可控变点”为点P3(x,﹣y),点P3(x,﹣y)的“可控变点”为点P4(﹣x,﹣y),点P4(﹣x,﹣y)的“可控变点”为点P5(x,y),…,故每四次变化出现一次循环;
当x<0时,同理可得每四次变化出现一次循环;
∵2018=4×504+2,
∴当点P2018的坐标为(3,a),则点P1的坐标为(﹣3,﹣a),
故答案为:(﹣3,﹣a);
(3)由题意知,点M的横坐标为﹣a.
当﹣a≥0时,a≤0,此时点M(﹣a,3).
代入y=﹣x+4,得3=a+4,a=﹣1,符合题意,
∴点M的坐标为(1,3);
当﹣a<0时,a>0,此时点M(﹣a,﹣3).
代入y=﹣x+4,得﹣3=a+4,a=﹣7,不合题意,舍去.
综上所述,点M的坐标为(1,3).


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有4个不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.
(1)请用树形图法或列表法,表示某个同学抽签的各种可能情况.
(2)小张同学对物理的①、②和化学的b、c号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
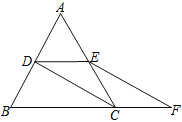
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连结CD和EF.
BC,连结CD和EF.
(1)求证:四边形CDEF是平行四边形;
(2)求四边形BDEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输部门规定:办理托运,当一件物品的重量不超过![]() 千克时,需付基础费
千克时,需付基础费![]() 元和保险费
元和保险费![]() 元;为了限制过重物品的托运,当一件物品的重量超过
元;为了限制过重物品的托运,当一件物品的重量超过![]() 千克时,除了付以上基础费和保险费外,超过部分每千克还需付
千克时,除了付以上基础费和保险费外,超过部分每千克还需付![]() 元的超重费.设某件物品的重量为
元的超重费.设某件物品的重量为![]() 千克,支付费用为
千克,支付费用为![]() 元.
元.
(1)当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
(2)甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:
托运人 | 物品重量/千克 | 支付费用/元 |
甲 | 14 | 33 |
乙 | 20 | 39 |
丙 | 30 |
|
根据以上提供的信息确定![]() 的值,并计算出丙所支付的费用
的值,并计算出丙所支付的费用![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:
(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )

A.2个 B.3个 C.4个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了备战初三物理、化学实验操作考试.某校对初三学生进行了模拟训练.物理、化学各有4个不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定.小张同学对物理的①、②和化学的b、c实验准备得较好,请用树形图或列表法求他两科都抽到准备得较好的实验题目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工厂今年一月份产量相同,都是a吨,三月份的产量也相同,甲厂每月产量增长的百分数(和上月相比)相同,乙厂每月产量增长的吨数(和上月相比)相同
(1)如果上述百分数是20%,那么甲厂三月份产量是多少?(结果可以含有a)
(2)如果上述百分数是-20%,那么乙厂二月份产量是多少?(结果可以含有a)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com