
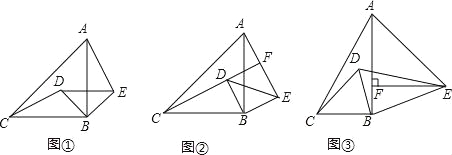
����Ŀ���Ķ����֣���1����ͼ�٣���Rt��ABC��Rt��DBE�У���ABC=��DBE=90�㣬AB=BC=3��BD=BE=1������CD��AE����֤����BCD�ա�BAE��������Ҫ֤����
������⣺��2���ڣ�1���������£���BD��AEʱ���ӳ�CD��AE�ڵ�F����ͼ�ڣ���AF�ij���
������⣺��3����ͼ�ۣ���Rt��ABC��Rt��DBE�У���ABC=��DBE=90�㣬��BAC=��DEB=30�㣬����CD��AE������BAE=45��ʱ����E��AB�ľ���EF�ij�Ϊ2�����߶�CD�ij�Ϊ ��
���𰸡���2��AF=2![]() ��1��
��1��
��3��![]() ��
��
��������
�����������2������BCD�ա�BAE���õ���OAF=��OCB�����ݡ�8���͡�֤����AFO=��CBO=90�㣬��RT��BDC�����ù��ɶ������CD����֤��BD=EF���ɽ�����⣮
��3���������߳ɱ����н���������������ƣ�����֤����ABE�ס�CBD����![]() �������AE���ɽ�����⣮
�������AE���ɽ�����⣮
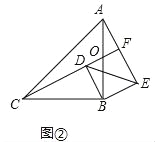
�����������2����ͼ���У�AB��CF���ڵ�O��
�ɣ�1����֪����BCD�ա�BAE��
���OAF=��OCB��CD=AE���ߡ�AOF=��COB��
���AFO=��CBO=90�㣬
��CF��AE����BD��AE��
��BD��CF��
��RT��CDB�У��ߡ�CDB=90�㣬BC=3��BD=1��
��CD=AE=![]() =2
=2![]() ��
��
�ߡ�BDF=��DFE=��DBE=90�㣬
���ı���EFDB�Ǿ��Σ�
��EF=BD=1��
��AF=AE��EF=2![]() ��1��
��1��
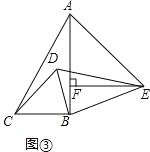
��3����RT��ABC��RT��EBD�У��ߡ�ABC=��DBE=90�㣬��BAC=��DEB=30�㣬
��AB=![]() BC��BE=
BC��BE=![]() BD��
BD��
��![]() ��
��
�ߡ�ABC=��EBD=90�㣬
���ABE=��DBC��
���ABE�ס�CBD��
��![]() ��
��
��RT��AEF�У��ߡ�AFE=90�㣬��EAF=45�㣬EF=2��
��AF=EF=2��AE=2![]() ��
��
��![]() ��
��
��CD=![]() ��
��
�ʴ�Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���д����˶��ᣬ��Ҫ�ڳ����꼶ѡȡ1��2��ͬѧ��Ϊ־Ը�ߣ�������5�����С�ܡ�С�ֺͳ�����6�����Сì��С��4��ͬѧ�����μӣ�
��1��������4��ͬѧ�����ѡȡ1��־Ը�ߣ���ѡ�е�����ͬѧǡ���dz�����5����ͬѧ�ĸ����� ��
��2��������4��ͬѧ�����ѡȡ2��־Ը�ߣ������оٷ�������״ͼ���б�������2��ͬѧǡ�ö��dz�����6����ͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
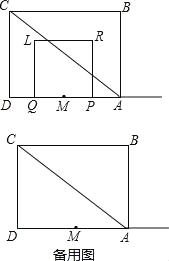
����Ŀ����ͼ���ı���ABCDΪ���Σ�ACΪ�Խ��ߣ�AB=6��BC=8����M��AD���е㣬P��Q����ͬʱ�ӵ�M��������P������MA�����˶�����Q���߶�MD�������˶�����D���������˶�����Mֹͣ����P��ֹ֮ͣ�˶���P��Q�����˶����ٶȾ�Ϊÿ��1����λ����PQΪһ��������������PRLQ�����P���˶�ʱ��Ϊt���룩��������PRLQ����ABC�ص����ֵ����ΪS��
��1������R���߶�AC��ʱ�����t��ֵ��
��2�����S��t֮��ĺ�����ϵʽ����ֱ��д��ȡֵ��Χ����������ϵʽʱ��ֻ��д���ص�����Ϊ������ʱ����ϸ���̣��������ֱ��д��������ϵʽ����
��3���ڵ�P����Q�˶���ͬʱ����һ��E��ÿ��1����λ���ٶȴ�C��B�˶�����tΪ��ֵʱ����LRE�ǵ��������Σ���ֱ��д��t��ֵ��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֵĵ���ά��Ҫ��30ǧ��Զ�Ľ������е������ޣ�����������Ħ�г����ߣ�15���Ӻ�����װ����������ϳ������������ͬʱ�����֪�������ٶ���Ħ�г���1.5�����������ֳ����ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ÿ�ѧ��������ʾ180 000�Ľ���ǣ� ��
A.18��104B.0.18��105C.1.8��105D.1.8��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ����Ͳ���ʽ
��1���ⷽ���� ![]()
��2���ⲻ��ʽ5x+15��4x+13���������ϱ�ʾ���Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ע�����������ʧ�෴��Ҫ����������֮������˼�ǣ������������������෴����ֱ���������븺����������Ϊ����8���Ϊ8�棬��-2���ʾ����Ϊ��������
A. ����2�� B. ����2�� C. ����6�� D. ����6��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com