
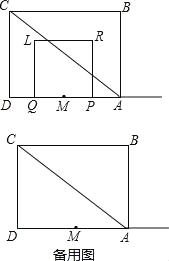
����Ŀ����ͼ���ı���ABCDΪ���Σ�ACΪ�Խ��ߣ�AB=6��BC=8����M��AD���е㣬P��Q����ͬʱ�ӵ�M��������P������MA�����˶�����Q���߶�MD�������˶�����D���������˶�����Mֹͣ����P��ֹ֮ͣ�˶���P��Q�����˶����ٶȾ�Ϊÿ��1����λ����PQΪһ��������������PRLQ�����P���˶�ʱ��Ϊt���룩��������PRLQ����ABC�ص����ֵ����ΪS��
��1������R���߶�AC��ʱ�����t��ֵ��
��2�����S��t֮��ĺ�����ϵʽ����ֱ��д��ȡֵ��Χ����������ϵʽʱ��ֻ��д���ص�����Ϊ������ʱ����ϸ���̣��������ֱ��д��������ϵʽ����
��3���ڵ�P����Q�˶���ͬʱ����һ��E��ÿ��1����λ���ٶȴ�C��B�˶�����tΪ��ֵʱ����LRE�ǵ��������Σ���ֱ��д��t��ֵ��ȡֵ��Χ��
���𰸡���1��t=![]() ��
��
��2��S��t֮��ĺ�����ϵʽΪ��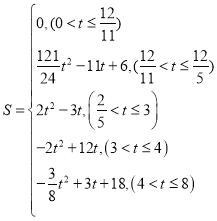 ��
��
��3��t��ȡֵ��Χ��4��t��8ʱ����LRE�ǵ��������Σ���t=4s����t=8s��![]() s��
s��![]() sʱ����LRE�ǵ��������Σ�
sʱ����LRE�ǵ��������Σ�
��������
�����������1���������������ƿɵ�![]() ����
����![]() ����ɣ�
����ɣ�
��2�����ݵ�P�͵�Q���˶������������۽�ɣ�
��3��������LRE�ǵ��������������������
�����������1������R���߶�AC��ʱ��Ӧ�����㣺![]() ��
��
��MPΪt����PR=2t��AP=4��t��
���ɵã�![]() ����
����![]() ��
��
��ã�t=![]() ��
��
��2����![]() ʱ��������PRLQ����ABCû���ص����֣������ص����ֵ����Ϊ0��
ʱ��������PRLQ����ABCû���ص����֣������ص����ֵ����Ϊ0��
��![]() ʱ��������PRLQ����ABC�ص����ֵ����Ϊֱ��������KRW�����=
ʱ��������PRLQ����ABC�ص����ֵ����Ϊֱ��������KRW�����=![]() ��
��
![]() ��
��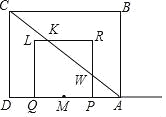
��![]() ʱ��������PRLQ����ABC�ص����ֵ����=
ʱ��������PRLQ����ABC�ص����ֵ����=![]() ����2t��3��2t=2t2��3t��
����2t��3��2t=2t2��3t��
��3��t��4ʱ��������PRLQ����ABC�ص����ֵ����=![]() ����12��2t����2t=��2t2+12t��
����12��2t����2t=��2t2+12t��
��4��t��8ʱ��������PRLQ����ABC�ص����ֵ����ΪS=![]() ��
��
��������S��t֮��ĺ�����ϵʽΪ��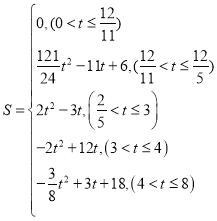 ��
��
��3���ڵ�P����Q�˶���ͬʱ����һ��E��ÿ��1����λ���ٶȴ�C��B�˶���
�ٵ���E��BC���е�ʱ����E��LR���д�������ʱ��EL=ER����ʱt=4s����LRE�ǵ��������Σ�
����E���B�غ�ʱ����E��LR���д�������ʱ��EL=ER����ʱt=8s����LRE�ǵ��������Σ�
����������t��ȡֵ��Χ��4��t��8��
�ڵ�EL=LRʱ����ͼ��ʾ��

LR=2t��CF=NL=4��t����EF=2t��4��FL=CN=6��2t��
����ֱ����EFL�У��ɹ��ɶ����õ���EL2=EF2+FL2=��2t��4��2+��6��2t��2��
����EL=LR�õ���EL2=LR2����4t2=10t2��40t+52��
��������
t2��10t+13=0��
��� t1=5+2![]() ����ȥ����t2=5��2
����ȥ����t2=5��2![]() ��
��
���Ե�t=5��2![]() ��s��ʱ����LRE�ǵ��������Σ�
��s��ʱ����LRE�ǵ��������Σ�
ͬ������ER=LRʱ��![]() ��
��
����������t��ȡֵ��Χ��4��t��8ʱ����LRE�ǵ��������Σ���t=4s����t=8s��![]() s��
s��![]() sʱ����LRE�ǵ��������Σ�
sʱ����LRE�ǵ��������Σ�
����;�ı����ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C��90����AC��4��BC��3��AB��5������AX��ֱ��AC����AΪ���㣬һ������Ϊ5���߶�PQ�������˵�P��Q�ֱ��ڱ�AC������AX���˶�����AP��___________ ʱ����ABC����PQAȫ�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������䣺��1����������������������2������������������3�����е�����������������4�����������У����˸�������������������ȷ���������У�������.
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������һ�����Ի�������y��2xͼ�����()
A. (0��0)��(2��1) B. (0��0)��(1��2)
C. (1��2)��(2��1) D. (��1��2)��(1��2)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������й����Żݻ�� ��һ���Թ��鲻����100Ԫ�������ܴ����Żݣ�
��һ���Թ��鳬��100Ԫ��������200Ԫһ�ɴ���ۣ�
��һ���Թ��鳬��200Ԫһ�ɴ����ۣ�
С������λ�У����ι����ܹ�����229.4Ԫ���ڶ��ι���ԭ���ǵ�һ�ι���ԭ�۵�3������ôС�������ι���ԭ�۵��ܺ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
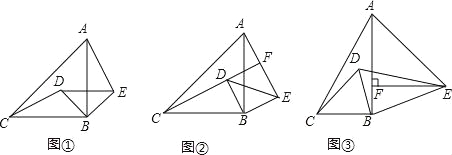
����Ŀ���Ķ����֣���1����ͼ�٣���Rt��ABC��Rt��DBE�У���ABC=��DBE=90�㣬AB=BC=3��BD=BE=1������CD��AE����֤����BCD�ա�BAE��������Ҫ֤����
������⣺��2���ڣ�1���������£���BD��AEʱ���ӳ�CD��AE�ڵ�F����ͼ�ڣ���AF�ij���
������⣺��3����ͼ�ۣ���Rt��ABC��Rt��DBE�У���ABC=��DBE=90�㣬��BAC=��DEB=30�㣬����CD��AE������BAE=45��ʱ����E��AB�ľ���EF�ij�Ϊ2�����߶�CD�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y=��x��2��2+3��ͼ������ƽ��3����λ��������ƽ��2����λ�����ö��κ����Ľ���ʽΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com