
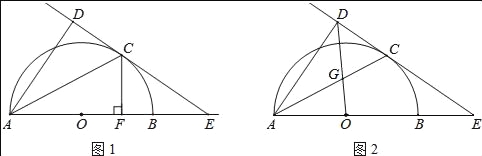
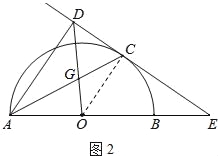
【题目】如图1,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图2,连接OD交AC于点G,若![]() =
=![]() ,求sin∠E的值.
,求sin∠E的值.
【答案】(1)见解析;
(2)CF=![]() ;
;
(3)sin∠E=![]() .
.
【解析】
试题分析:(1)连结OC,如图1,根据切线的性质得OC⊥DE,而AD⊥DE,根据平行线的性质得OC∥AD,所以∠2=∠3,加上∠1=∠3,则∠1=∠2,所以AC平分∠DAB;
(2)如图1,由B为OE的中点,AB为直径得到OB=BE=2,OC=2,在Rt△OCE中,由于OE=2OC,根据含30度的直角三角形三边的关系得∠OEC=30°,则∠COE=60°,由CF⊥AB得∠OFC=90°,所以∠OCF=30°,再根据含30度的直角三角形三边的关系得OF=![]() OC=1,CF=
OC=1,CF=![]() OF=
OF=![]() ;
;
(3)连结OC,如图2,先证明△OCG∽△DAG,利用相似的性质得![]() =
=![]() =
=![]() ,再证明△ECO∽△EDA,利用相似比得到
,再证明△ECO∽△EDA,利用相似比得到![]() =
=![]() =
=![]() ,设⊙O的半径为R,OE=x,代入求得OE=3R;最后在Rt△OCE中,根据正弦的定义求解.
,设⊙O的半径为R,OE=x,代入求得OE=3R;最后在Rt△OCE中,根据正弦的定义求解.
试题解析:(1)连结OC,如图1,∵DE与⊙O切于点C,∴OC⊥DE,
∵AD⊥DE,∴OC∥AD,∴∠2=∠3,∵OA=OC,∴∠1=∠3,
∴∠1=∠2,
即AC平分∠DAB;
(2)如图1,
∵直径AB=4,B为OE的中点,
∴OB=BE=2,OC=2,
在Rt△OCE中,OE=2OC,
∴∠OEC=30°,
∴∠COE=60°,∵CF⊥AB,∴∠OFC=90°,∴∠OCF=30°,∴OF=![]() OC=1,CF=
OC=1,CF=![]() OF=
OF=![]() ;
;
(3)连结OC,如图2,∵OC∥AD,∴△OCG∽△DAG,∴![]() =
=![]() =
=![]() ,∵OC∥AD,
,∵OC∥AD,
∴△ECO∽△EDA,∴![]() =
=![]() =
=![]() ,设⊙O的半径为R,OE=x,∴
,设⊙O的半径为R,OE=x,∴![]() =
=![]() ,解得OE=3R,
,解得OE=3R,
在Rt△OCE中,sin∠E=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某车间有26名工人,每人每天可以生产800个螺钉或1 000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套.设安排x名工人生产螺钉,则下面所列方程正确的是( )
A. 2×1 000(26-x)=800x B. 1 000(13-x)=800x
C. 1 000(26-x)=2×800x D. 1 000(26-x)=800x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com