
分析 (1)直接利用绝对值的性质以及结合零指数幂的性质和负整数指数幂的性质化简求出答案;
(2)直接利用幂的乘方运算法则以及同底数幂的乘法运算法则分别化简求出答案;
(3)直接利用单项式乘以多项式运算法则化简求出答案;
(4)直接利用幂的乘方运算法则化简求出答案.
解答 解:(1)|-1|+(-2)3+(7-π)0-($\frac{1}{3}$)-1
=1-8+1-3
=-9;
(2)(-a2)3-6a2•a4
=-a6-6a6
=-7a6;
(3)3x-2(x-1)-3(x+1)
=3x-2x+2-3x-3
=-2x-1;
(4)(m4)2+m5•m3+(-m)4•m4
=m8+m8+m8
=3m8.
点评 此题主要考查了同底数幂的乘法运算以及幂的乘方运算、实数运算等知识,正确掌握运算法则是解题关键.


科目:初中数学 来源: 题型:解答题
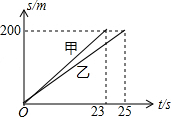 如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题:
如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察图,先填空,然后回答问题.
观察图,先填空,然后回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
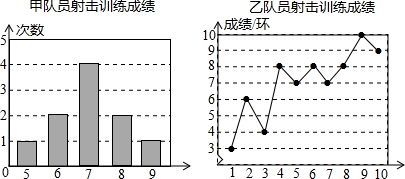
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | 7 | 7 | 7 | 1.2 |
| 乙 | 7 | 7.5 | 8 | 4.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{12b}{{27{a^2}}}$ | B. | $\frac{{2{{(a-b)}^2}}}{b-a}$ | C. | $\frac{{{x^2}+{y^2}}}{x+y}$ | D. | $\frac{{{x^2}-{y^2}}}{x-y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
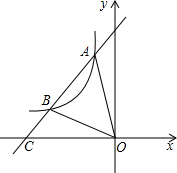 如图,直线y1=kx+b与反比例函数y2=$\frac{k′}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
如图,直线y1=kx+b与反比例函数y2=$\frac{k′}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com