练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知：代数式-2x2+4x-18（1）请用配方法证明此代数式的值总是负数．（2）你觉得此代数式有最大值吗？若有，请你求出它的最大值；若没有，请说明你的理由．

    分析 （1）根据配方法的步骤把代数式-2x2+4x-18进行配方，即可得出答案；
    （2）根据（1）的结果即可直接得出代数式的最大值．

    解答 （1）证明：∵-2x2+4x-18=-2（x2-2x+9）=-2（x2-2x+1+8）=-2（x-1）2-16，
    -2（x-1）2≤0，
    ∴-2（x-1）2-16＜0，
    ∴-2x2+4x-18无论x取何值，代数式的值总是负数；

    （2）解：∵-2x2+4x-18=-2（x-1）2-16，
    ∴当x=1时，代数式有最大值，最大值是-16．

    点评 此题考查了配方法的应用，用到的知识点是配方法的步骤，关键是对要求的式子进行配方，注意在变形的过程中不要改变式子的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

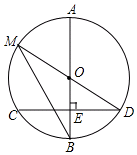    7．如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB．
    （1）若CD=16，BE=4，求⊙O的直径；
    （2）若∠M=∠D，求∠D的度数．
    （3）在（2）的条件下，求$\widehat{BD}$的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．解方程
    （1）8x=12（x-2）；                      
    （2）$\frac{0.1x-0.2}{0.02}$-$\frac{x+1}{0.5}$=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，四边形ABCD是圆内接四边形，AD，BC的延长线相交于点P，∠APB的平分线交CD于点E，交AB于点F．
    求证：∠CEF=∠BFE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知，⊙O的半径为1，BC为⊙O的弦，直径MN⊥BC（M在劣弧BC上），A为弧BN上一动点（不与B、N重合），∠BAC=60°
    （1）如图1，求BC的长；
    （2）如图2，D为AC上一点且CD=AB，E为BD中点，连AE，求AE的长；
    （3）如图3，在（2）的条件下，连BO，将BO绕B点顺时针旋转90°得到BF，当A在弧BN上运动时，EF的最小值为$\sqrt{2}$-$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：
    （1）$\frac{1}{2}$$\sqrt{12}$-（3$\sqrt{\frac{1}{3}}$+$\sqrt{2}$）；
    （2）$\frac{\sqrt{12}+\sqrt{3}}{\sqrt{3}}$+$\frac{\sqrt{8}×\sqrt{6}}{\sqrt{2}}$；
    （3）（3$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$）÷$\sqrt{32}$；
    （4）（$\sqrt{3}$-$\sqrt{2}$）2（5+2$\sqrt{6}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：102°21″43′÷3+20°15′33″．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

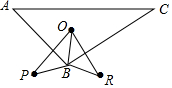    6．如图，O为△ABC内部一点，OB=3$\frac{1}{2}$，点O关于直线AB、直线BC的对称点分别为P、R．
    （1）请指出当∠ABC为多少度时，PR的长等于7？并说明理由；
    （2）请判断当∠ABC不是（1）中的角度时，PR的长度是小于7还是会大于7？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．计算
    （1）-9+13-3+8$\frac{1}{17}$                   
    （2）2$\frac{1}{7}$-3$\frac{2}{3}$-5$\frac{1}{3}$+（-3$\frac{1}{7}$）
    （3）1÷（-1$\frac{1}{2}$）-|-$\frac{5}{3}$|
    （4）（-2）×$\frac{3}{2}$÷|-$\frac{3}{4}$|×4
    （5）18×（-$\frac{2}{3}$）+13×$\frac{2}{3}$-4×$\frac{2}{3}$      
    （6）-100$\frac{98}{99}$×99．

    查看答案和解析>>

    同步练习册答案