
分析 (1)首先化简二次根式,进而合并同类二次根式得出答案;
(2)首先化简二次根式,进而合并同类二次根式得出答案;
(3)首先化简二次根式,进而合并同类二次根式得出答案;
(4)直接利用完全平方公式以及平方差公式化简求出答案.
解答 解:(1)$\frac{1}{2}$$\sqrt{12}$-(3$\sqrt{\frac{1}{3}}$+$\sqrt{2}$)
=$\frac{1}{2}$×2$\sqrt{3}$-$\sqrt{3}$-$\sqrt{2}$
=-$\sqrt{2}$;
(2)$\frac{\sqrt{12}+\sqrt{3}}{\sqrt{3}}$+$\frac{\sqrt{8}×\sqrt{6}}{\sqrt{2}}$
=$\frac{3\sqrt{3}}{\sqrt{3}}$+$\frac{2\sqrt{2}×\sqrt{6}}{\sqrt{2}}$
=3+2$\sqrt{6}$;
(3)(3$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$)÷$\sqrt{32}$
=(9$\sqrt{2}$+$\sqrt{2}$-2$\sqrt{2}$)÷4$\sqrt{2}$
=2;
(4)($\sqrt{3}$-$\sqrt{2}$)2(5+2$\sqrt{6}$)
=(5-2$\sqrt{6}$)(5+2$\sqrt{6}$)
=25-24
=1.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | y=(x+1)2-13 | B. | y=(x-5)2-3 | C. | y=(x-5)2-13 | D. | y=(x+1)2-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的差值(单位:克) | -4 | -2 | 0 | +1 | +3 | +5 |
| 袋数 | 1 | 3 | 6 | 4 | 4 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,D为$\widehat{AB}$的中点,C为$\widehat{AD}$上一点,弦CD=$\sqrt{2}$,I为△ABC内心.
如图,AB为⊙O的直径,D为$\widehat{AB}$的中点,C为$\widehat{AD}$上一点,弦CD=$\sqrt{2}$,I为△ABC内心.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
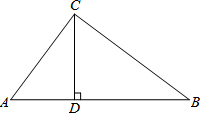 如图,在△ABC中,CD⊥AB于D点,AB=22,CD=8,tanA=$\frac{4}{3}$,求:
如图,在△ABC中,CD⊥AB于D点,AB=22,CD=8,tanA=$\frac{4}{3}$,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com