
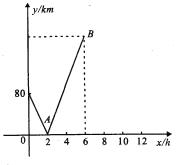
【题目】甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1h后,快车才开始行驶,已知快车的速度是120km/h,以快车开始行驶计时,设时间为x(h),两车之间的距离为y(km),图中的折线是y与x的函数关系的部分图象.根据图象解决下列问题:
(1)慢车的速度是 km/h,点B的坐标是 .
(2)求线段AB所表示的y与x之间的函数关系式.
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=![]() x2+2x+6的图像与x轴相交于A、B两点,与y轴交于点C,顶点为点D,该二次函数图像的对称轴与直线BC相交于点E,与x轴交于点F;
x2+2x+6的图像与x轴相交于A、B两点,与y轴交于点C,顶点为点D,该二次函数图像的对称轴与直线BC相交于点E,与x轴交于点F;
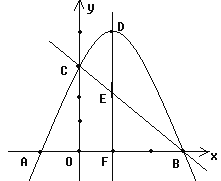
(1)求直线BC的解析式;
(2)试判断△BFE与△DCE是否相似?并说明理由.
(3)在坐标轴上是否存在这样的点P,使得以点P、B、C为顶点的三角形与△DCE相似?若存在,请求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列证明过程填空:
已知:如 图,AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2.
求证:AD平分∠BAC,填写证明中的空白.
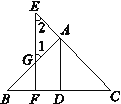
证明:
∵AD⊥BC,EF⊥BC (已知),
∴EF∥AD ( ),
∴_______ _ = ________ ( 两直线平行,内错角相等 ),
________ =∠CAD ( ____________ ).
∵________ (已知),
∴________ ,即AD平分∠BAC ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A(﹣4,y1),B(﹣3,y2),C(1,y3)为二次函数y=x2+4x﹣5的图象上的三点,则y1,y2,y3的大小关系是( )
A. y1<y2<y3 B. y2<y1<y3 C. y3<y1<y2 D. y1<y3<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程 x2﹣2x+k=0.
(1)若原方程有实数根,求k的取值范围?
(2)选取一个你喜欢的非零整数值作为k的值,使原方程有实数根,并解方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
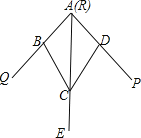
【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
A.SAS
B.ASA
C.AAS
D.SSS
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com