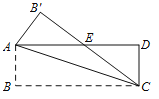
【题目】如图，矩形ABCD中，AB＝2 cm，BC＝6cm，把△ABC沿对角线AC折叠，得到△AB’C，且B’C与AD相交于点E，则AE的长为___cm．

参考答案：

【答案】

【解析】先根据等角对等边，得出AE=CE，再设AE=CE=x，在Rt△CDE中，根据勾股定理列出关于x的方程，求得x的值即可．

解：由折叠得，∠BCA=∠ACB′，

由AD∥BC得，∠BCA=∠CAD，

∴∠ACB′=∠CAD，

∴AE=CE，

设AE=CE=x，则DE=6–x，

在Rt△CDE中，DE2+CD2=CE2，即（6–x）2+22=x2，

解得x=，

∴AE的长为cm．

故答案为：．

“点睛”本题以折叠问题为背景，主要考查了轴对称的先行者以及勾股定理，折叠是一种对称变换，它属于轴对称，折叠前后的对应边和对应角相等. 解题时，我们常设所求的线段长为x，然后用含x 的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求解.

关闭