
【题目】已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c.
(1)试判断△ABC的形状.
(2)求AB边上的高。
【答案】(1)直角三角形;(2)![]() .
.
【解析】
把a2+b2-c2+338=10a+24b+26c化为(a-5)2+(b-12)2-(c-13)2=0,根据非负数的性质求得a、b、c的值,再利用勾股定理的逆定理判断△ABC为直角三角形即可;(2)利用直角三角形面积的两种表示法求得AB边上的高即可.
(1)∵a2+b2-c2+338=10a+24b+26c,
∴a2-10a+25+b2-24b+144-c2-26c+169=0,
∴(a-5)2+(b-12)2+(c-13)2=0,
即a=5,b=12,c=13(a,b,c都是正的),
∵52+122=132,
∴该三角形是直角三角形,且∠ACB=90°.
(2)设AB边上的高为h,
根据直角三角形面积的两种表示法可得,![]() ,
,
即![]() ,
,
解得h=![]() .
.
∴AB边上的高为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD//BC和AB//CD.请完成下面的推理过程,填写理由或数学式:

∵∠1=∠2,∠1=∠AGH(_________)
∴∠2=∠AGH(________)
∴AD//BC(________)
∴∠ADE=∠C(________)
∵∠A=∠C(已知)
∴∠ADE=_______(等量代换)
∴AB//CD(_______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8,BC=10,以B为圆心,任意长为半径画弧分别交BA、BC于点M和N,再分别以M、N为圆心,大于 ![]() MN长为半径画弧,两弧交于点P,连结BP并延长交AC于点D,若△BDC的面积为20,则△ABD的面积为( )
MN长为半径画弧,两弧交于点P,连结BP并延长交AC于点D,若△BDC的面积为20,则△ABD的面积为( ) 
A.20
B.18
C.16
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动.小明从学校同学中随机抽取一部分同学,对他们参加锻炼的情况进行了统计,并绘制了下面的图1和图2,请根据所绘制的统计图回答下面问题: 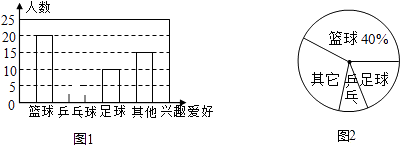
(1)在此次调查中,小明共调查了位同学;
(2)请在图1中将“乒乓球”部分的图形补充完整;
(3)图2中表示“足球”的扇形的圆心角的度数为度;
(4)如果该学校共有学生2500人,则参加“篮球”运动项目的人数约有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:

(1)2018在第________行,第________列;
(2)由五个数组成的“![]() ”中:
”中:
① 这五个数的和可能是2019吗,为什么?
② 如果这五个数的和是60,直接写出这五个数;
(3)如果这五个数的和能否是2025,若能请求出这5个数;若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y= ![]() x+1与抛物线y=ax2+bx﹣3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D
x+1与抛物线y=ax2+bx﹣3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D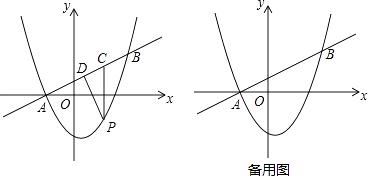
(1)①求抛物线的解析式;②求sin∠ACP的值
(2)设点P的横坐标为m
①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把△PDB分成两个三角形,求出当这两个三角形面积之比为9:10时的m值;
③是否存在适合的m值,使△PCD与△PBD相似?若存在,直接写出m值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知边长为4的正方形ABCD,P是BC边上一动点(与B、C不重合),连结AP,作PE⊥AP交∠BCD的外角平分线于E.设BP=x,△PCE面积为y,则y与x的函数关系式是( )
A.y=2x+1
B.y= ![]() x﹣2x2
x﹣2x2
C.y=2x﹣ ![]() x2
x2
D.y=2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com