
【题目】如图:

(1)2018在第________行,第________列;
(2)由五个数组成的“![]() ”中:
”中:
① 这五个数的和可能是2019吗,为什么?
② 如果这五个数的和是60,直接写出这五个数;
(3)如果这五个数的和能否是2025,若能请求出这5个数;若不能请说明理由.
【答案】(1)225,2;(2)①不可能;②3,11,12,13,21;(3)不存在.
【解析】
(1)观察规律,每行9个数,2018÷9=224……2,所以2018在225行,第2列;
(2)①通过观察可知,这五个数的和是中间数的5倍,而2019不是5的倍数;
②中间数是12,根据图直接写出即可;
(3)中间数是405,405在第45行末尾,不可能是中间数.
(1)225,2;
(2) ①不可能,因为这五个数的和是中间数的5倍,而2019不是5的整数倍,所以这五个数的和不可能是2019.
②3,11,12,13,21;
(3)因为2025=5×405,而405=9×45,所以405在第45行,第9列,所以不存在.
故答案为:(1)225,2;(2)①不可能;②3,11,12,13,21;(3)不存在.


科目:初中数学 来源: 题型:
【题目】如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于E点. 
(1)求证:四边形OECD是菱形;
(2)若AB=4,AC=8,求菱形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在⊙O中, ![]() =
= ![]() ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC. 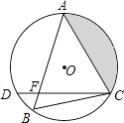
(1)求证:AC2=ABAF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c.
(1)试判断△ABC的形状.
(2)求AB边上的高。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正三角形中,将其内切圆和三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则此三角形剩下部分(阴影部分)的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并填空:
寻求某些勾股数的规律:
⑴对于任何一组已知的勾股数都扩大相同的正整数倍后,就得到了一组新的勾股数.例如:![]() ,我们把它扩大2倍、3倍,就分别得到
,我们把它扩大2倍、3倍,就分别得到![]() 和
和![]() ,……若把它扩大11倍,就得到 ,若把它扩大n倍,就得到 .
,……若把它扩大11倍,就得到 ,若把它扩大n倍,就得到 .
⑵对于任意一个大于1的奇数,存在着下列勾股数:
若勾股数为3,4,5,因为,则有![]() ;
;
若勾股数为5,12,13,则有![]() ;
;
若勾股数为7,24,25,则有 ;……
若勾股数为m(m为奇数),n, ,则有m2= ,用m来表示n= ;
当m=17时,则n= ,此时勾股数为 .
⑶对于大于4的偶数:
若勾股数为6,8,10,因为![]() ,则有……请找出这些勾股数之间的关系,并用适当的字母表示出它的规律来,并求当偶数为24的勾股数.
,则有……请找出这些勾股数之间的关系,并用适当的字母表示出它的规律来,并求当偶数为24的勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“美丽广西,清洁乡村”活动中,李家村村长提出了两种购买垃圾桶方案;方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元;设方案1的购买费和每月垃圾处理费共为y1元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为y2元,交费时间为x个月.
(1)直接写出y1、y2与x的函数关系式;
(2)在同一坐标系内,画出函数y1、y2的图象;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com